Начальная скорость:  м/с.
м/с.
Высота:  м.
м.
Найти нужно время: 
1. Тело движется против силы притяжения, его движение - равнозамедленное. Тогда высота, на которой тело будет находиться в момент времени t, будет выражаться формулой: 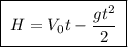
2. Чтобы найти из (1) время нужно решить квадратное уравнение относительно t:
![\dfrac{g}{2}t^2 - V_0t + H = 0,\\\\D = \left[b^2 - 4ac\right] = V_0^2 - \dfrac{4Hg}{2} = V_0^2 - 2gH.\\t_{1,2} = \left[\dfrac{-b\pm\sqrt{D}}{2a}\right] = \dfrac{V_0\pm\sqrt{V_0^2 - 2gH}}{g}.](/tpl/images/0436/9987/3c593.png)
3. Таким образом получаем два решения, потому как дело достигнет высоты 10 метров дважды - во время подъёма до максимальной высоты и во время падения. Нас интересует первое прохождение данной отметки, поэтому вычислим меньшее из значений: 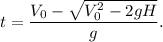
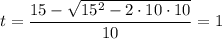 (c).
(c).