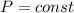 ) среднюю теплоёмкость сухих компонент воздуха, равную
) среднюю теплоёмкость сухих компонент воздуха, равную 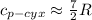 , и изобарную теплоёмкость пара, равную
, и изобарную теплоёмкость пара, равную 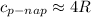 , поскольку сухая компонента воздуха преимущественно двухатомная, а пар – трёхатомный.
, поскольку сухая компонента воздуха преимущественно двухатомная, а пар – трёхатомный.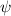 – количество вещества СУХИХ КОМПОНЕНТ ВОЗДУХА.
– количество вещества СУХИХ КОМПОНЕНТ ВОЗДУХА.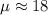 г/моль
г/моль 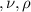 и
и 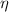 – молярная масса, количество вещества, парциальная плотность ВОДЯНОГО ПАРА и относительная влажность.
– молярная масса, количество вещества, парциальная плотность ВОДЯНОГО ПАРА и относительная влажность.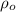 – парциальная плотность НАСЫЩЕННОГО водяного пара.
– парциальная плотность НАСЫЩЕННОГО водяного пара.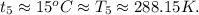
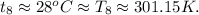
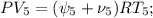

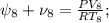
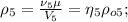
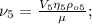
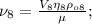
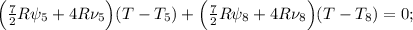
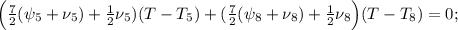
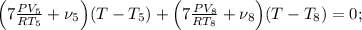
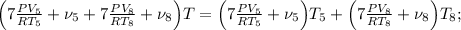
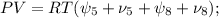
![\frac{PV}{R} \Big( 7 \frac{PV_5}{RT_5} + \nu_5 + 7 \frac{PV_8}{RT_8} + \nu_8 \Big) =\\\\= ( \psi_5 + \nu_5 + \psi_8 + \nu_8 ) \Big[ \Big( 7 \frac{PV_5}{RT_5} + \nu_5 \Big) T_5 + \Big( 7 \frac{PV_8}{RT_8} + \nu_8 \Big) T_8 \Big] ;](/tpl/images/0679/6114/acb39.png)
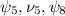 и
и 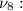
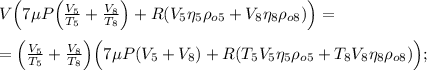




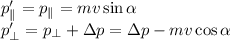
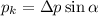
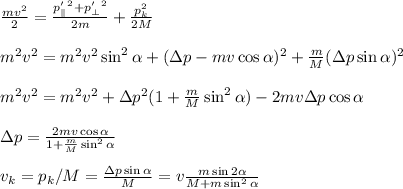
Если принебречь всеми поторями и считать, что автомобиль имеет скорость V2 = 20м/c на границе между горизонтальным участком и наклонной, то изходя из закона сохранения энергии имеем: