Объём "холодной" воды: V₁ = 0,5 л = 0,5 * 10⁻³ м³.
Температура холодной воды: t₁ = 20 °C.
Температура кипятка: t₂ = 100 °C.
Температура баланса: t = 80 °C.
Удельная теплоёмкость воды (из таблицы): c = 4200 Дж/(кг * °C).
Плотность воды (из таблицы): ρ = 1000 кг/м³.
* с и ρ и нам не понадобятся, но пусть будут, эту цифры лучше знать.
Найти нужно объём кипятка: V₂ - ?
Решение:0. Разберёмся с происходящим. Кипяток отдаёт тепло, холодная вода принимает его. В результате теплота остывания кипятка тратится на нагревание холодной воды. Как мы знаем, отданное тепло равняется полученному теплу.
1. Запишем уравнение теплового баланса:
Qотданное = Qполученное, или cm₁(t - t₁) = cm₂(t₂ - t).
2. Можем сократить на с, получим:
m₁(t - t₁) = m₂(t₂ - t).
3. Вспомним формулу массы: m = ρV.
4. Немного сократим формулу, полученную в (2):
pV₁(t - t₁) = pV₂(t₂ - t),
V₁(t - t₁) = V₂(t₂ - t).
5. Выразим объём кипятка:
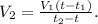
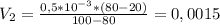 (м³).
(м³).
Переведём в литры: 0,0015 м³ = 1,5 л.
ответ: 1,5 л.ДАНО
Радиус Земли R=6400 км.
Радиус орбиты спутника R1
Ускорение свободного падения Земли g=10 м/с2.
РЕШЕНИЕ
пусть угловая скорость вращения Земли -w
если спутник проходит периодически над точкой запуска ровно через трое суток
то угловая скорость вращения спутника w1=2/3*w
ускорение свободного падения в точке запуска
g=GM/R^2
V^2/R=GM/R^2
w^2*R=GM/R^2
w^2=GM/R^3 (1)- это квадрат угловой скорости точки запуска
w1^2=GM/R1^3 (2) -это квадрат угловой скорости спутника
разделим (2) на (1)
w1^2/w^2=GM/R1^3/GM/R^3
(w1/w)^2=(R/R1)^3
R1/R=(w/w1)^(2/3) -подставим сюда w1=2/3*w
R1/R=(w/(2/3*w))^(2/3)=(3/2)^(2/3)=(9/4)^(1/3)=1.31 =1
ОТВЕТ R1/R=1