 , то движение является прямолинейным, а поэтому все движение будем рассматривать только вдоль оси
, то движение является прямолинейным, а поэтому все движение будем рассматривать только вдоль оси  , и все характеристики движения (векторы скорости, ускорения) будем рассматривать в виде проекций на ось
, и все характеристики движения (векторы скорости, ускорения) будем рассматривать в виде проекций на ось  . Из условия имеем, что
. Из условия имеем, что 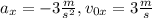 .
.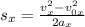 . В момент поворота тело имеет скорость
. В момент поворота тело имеет скорость 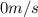 (то есть
(то есть 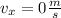 ), а начальная скорость и ускорение тела даны в условии. Воспользуемся данной формулой и найдем путь, пройденный телом до поворота:
), а начальная скорость и ускорение тела даны в условии. Воспользуемся данной формулой и найдем путь, пройденный телом до поворота: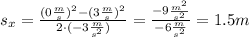 . Отлично. Путь, пройденный телом до поворота, мы нашли. Теперь же для дальнейших расчетов нам понадобится узнать время, за которое тело этот путь. Время узнаем из другой формулы:
. Отлично. Путь, пройденный телом до поворота, мы нашли. Теперь же для дальнейших расчетов нам понадобится узнать время, за которое тело этот путь. Время узнаем из другой формулы: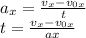
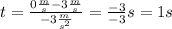 .
. 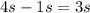 . На этот раз путь будем искать по другой формуле, не зависящей от конечной скорости (нам она теперь неизвеста):
. На этот раз путь будем искать по другой формуле, не зависящей от конечной скорости (нам она теперь неизвеста): 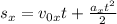
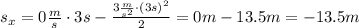
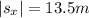
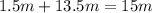

ускорение свободного падения
- на Земле g = GM / R^2
- на Планете g1 = G*(M/4) / (2R)^2 = 1/16 *GM / R^2 =g /16
ускорение свободного падения на планете - в 16 раз меньше, чем на Земле
g1 = 10/16 =0,625 м/с2