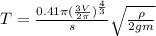
Объяснение:
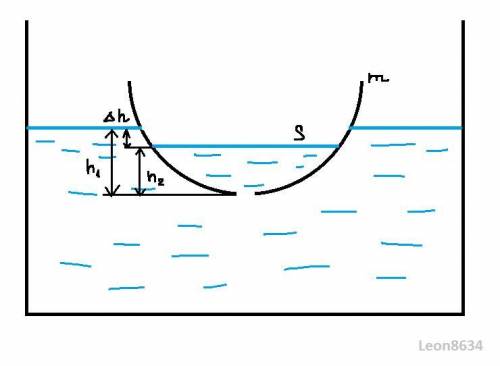
По мере погружения чаши создается перепад высот жидкости внутри и снаружи нее, этот перепад не позволяет ей утонуть мгновенно, выразим его пренебрегая толщиной стенок чаши
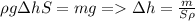 где S - площадь поверхности воды в чаше (в первом приближении).
где S - площадь поверхности воды в чаше (в первом приближении).
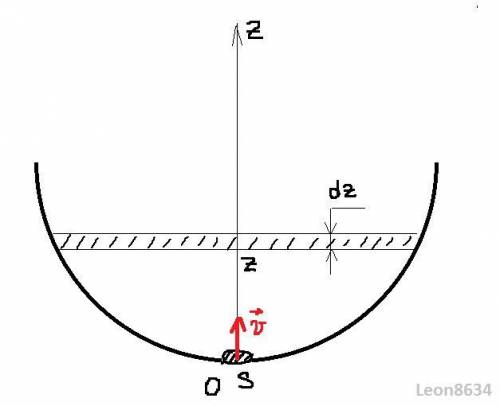
Пусть вода в чаше находится на уровне z и повысилась на малое dz, тогда из условия неразрывности потока можно записать
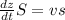
где S - площадь поверхности воды, а s - площадь отверстия.
Выразим площадь поверхности воды через z, для этого вспомним кое что из школы
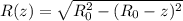
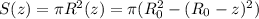
где R₀ - радиус чаши (можно найти из объема в конце)
Скорость втекания жидкости в отверстие найдем по формуле Торричелли
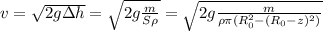
Подставляя все в дифференциальное уравнение получим
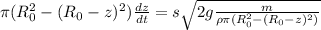
Несколько упростим
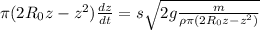
Попробуем разделить переменные
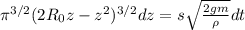
Проинтегрируем обе части
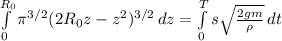
Левый интеграл находим не без "костылей", правый берется легко
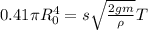
Откуда время вытекания
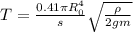
Осталось найти радиус, если объем чаши V объем всей сферы 2V отсюда
![\frac{4}{3}\pi R_0^3=2V = R_0=\sqrt[3]{\frac{3V}{2\pi } }](/tpl/images/1358/0931/d7f14.png)
Окончательно
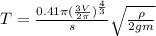 .
.
I2≈13,73 А
Объяснение:
До замыкания ключа ток I1 протекал только через R1 и был равен 7А
По закону Ома
I=U/R
7=U/75 , откуда
U=7*75=525 В
После замыкания ключа в схему подключаются дополнительные резисторы, и меняется ее общее сопротивление.
R3 и R2 соединены последовательно и имеют общее сопротивление R4
R4=R2+R3=33+45=78 Ом
R4 и R1 соединены параллельно, и общее сопротивление составит (для двух резисторов):
Rобщ=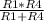 =
=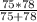 =5850/153 ≈38,24 Ом
=5850/153 ≈38,24 Ом
Тогда ток I2 протекающий через амперметр составит
I2=U/Rобщ=525/38,24≈13,73 А