По всей цепи протекает один и тот же ток I, так как н.с.1 и н.с.2 соединены между собой последовательно. Для определения тока в электрической цепи нужно построить результирующую ВАХ цепи. Для построения этой характеристики следует суммировать абсциссы кривых 1 и 2 (аг = аб + ав), соответствующие одним и те же значениям тока. Далее, задаваясь произвольным значением тока (например, больше I’ и меньше I’ ) можно построить ВАХ всей цепи (рис. 5.6, кривая 3).
При параллельном соединении двух нелинейных элементов (рис. 5.7) ток в неразветвленной части электрической цепи равен сумме токов в параллельных определенных ветвях. Поэтому при построении результирующей ВАХ всей цепи следует суммировать ординаты графиков 1 и 2 (рис. 5.8), соответствующие одним и те же значениям напряжения, так как к этим нелинейным элементам приложено одно и то же напряжение, равное напряжению внешней сети, т.е. источника питания. Например, для произвольного значения напряжения находим ординату аг точки для результирующей кривой 3. (аг = ав + аб)
Объяснение:
B1.
1. сопротивление проводника -- увеличится
2. сила тока -- уменьшится
3. выделяющаяся на проводнике мощность -- уменьшится
1) Формула для элекрического сопротивления: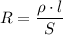
Из формулы видно, что при увеличении длины 
в 2 раза - сопротивление 
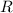тоже увеличится в 2 раза, эти величины прямопропорциональны.
2) По закону Ома сила тока определяется как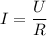
Напряжение осталось тем же, сопротивление увеличилось, значит сила тока уменьшилась в 2 раза.
3) Мощность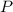 
определяется как произведение силы тока и напряжения: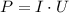
Сила тока уменьшилась, значит и мощность уменьшилась (при постоянном напряжении).
В2.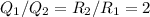 
По закону Джоуля-Ленца количество теплоты, выделяющееся в проводнике с сопротивлением при прохождении через него тока 
за время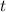 
определяется так: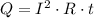
Воспользуемся законом Ома (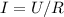
), чтобы переписать закон Джоуля-Ленца через напряжение: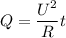
При параллельном соединении напряжение на каждом из резисторов одинаковое (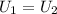
). Значит, количество выделенной теплоты будет определяться только в сопротивлением:
B3.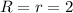 
Ом
Закон Ома для полной цепи с наличием ЭДС: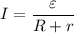
В первом случае имеем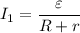
,
а во втором
.
Приведем каждое из этих уравнений к общему знаменателю и получим систему двух уравнений на 2 неизвестных - 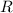и 
:
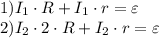
Подставим известные величины из условия задачи и получим: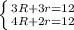
Решением являются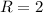 
и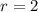 
.
В4. 3 А
При последовательном соединении резисторов сила тока одинакова:
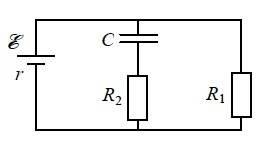
В5. 1.05 мКл (!)
Решение по рисунку схемы в приложении (!).
Емкость конденсатора 
определяется как 
. Отсюда, заряд конденсатора равен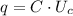 
. Осталось только понять, какое напряжение 
на конденсаторе. Из рисунка видно, что конденсатор и резистор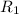 
соединены параллельно, то есть 
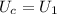. При этом ток 
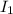через резистор 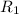равен полному току цепи, который можно определить по закону Ома для полной цепи:
.
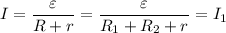Таким образом, можем найти напряжение на конденсаторе:
.
Теперь можем определить заряд на конденсаторе: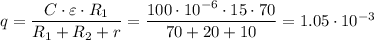
Кл = 1.05 мКл
2*A=h*c/L2 L2=h*c/2*A
L1/L2=2 L2=L1/2=2*10^-7/2=10^-7 м