820 кг/м³
Объяснение:
Вес Р равен силе реакции опоры N по определению. Поэтому разницу в весе будем считать через силу реакции опоры.
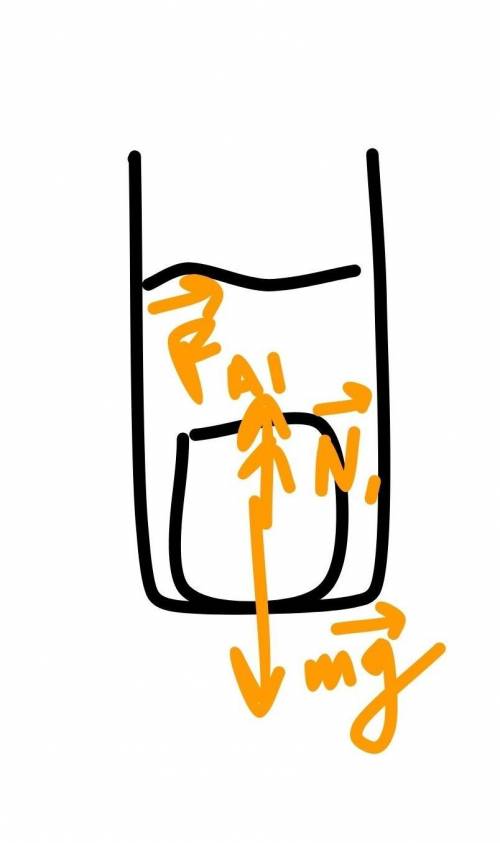
1) Для случая с водой (см рисунок):
N1 = mg - Fa1 = mg - ρ1*gV
Пластина стала легче = в отличии от исходного веса в воздухе, то есть:
N1 = mg - 50*10^(-3)
Объединяем:
mg - ρ1*gV = mg - 50*10^(-3)
ρ1*gV = 50*10^(-3) - единственная неизвестная отсюда это V, поэтому можно найти значение объема:
10³*10*V = 50*10^(-3)
V = 50*10^(-7) м³
2) Для случая с нефтью всё аналогично:
N2 = mg - 41*10^(-3)
mg - ρ2*gV = mg - 41*10^(-3)
ρ2*gV = 41*10^(-3) - неизвестный объем уже посчитан, поэтому можно выразить плотность нефти
ρ2 = 41*10^(-3) / gV = 41*10^(-3) / (10 * 50*10^(-7)) = 820 кг/м³
 – длина одного вагона или локомотива,
– длина одного вагона или локомотива,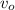 – скорость передней точки локомотива, когда он проезжает мимо,
– скорость передней точки локомотива, когда он проезжает мимо,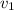 – скорость поезда, когда локомотив только что проехал наблюдателя,
– скорость поезда, когда локомотив только что проехал наблюдателя, – скорость поезда, когда только k вагонов ещё не проехали мимо,
– скорость поезда, когда только k вагонов ещё не проехали мимо, – скорость поезда, когда весь поезд проехал наблюдателя,
– скорость поезда, когда весь поезд проехал наблюдателя,
 наступило состояние
наступило состояние 
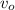 и
и  – отделаят промежуток времени
– отделаят промежуток времени 
 и
и  – очевидно отделаят промежуток времени
– очевидно отделаят промежуток времени 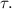
 [1]
[1]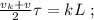 [2]
[2]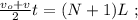 [3]
[3]
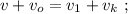 [4]
[4]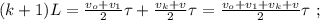
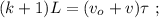
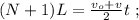
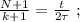
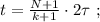 [5] – это всё время движения поезда мимо наблюдателя:
[5] – это всё время движения поезда мимо наблюдателя: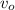 до значения
до значения 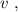 изменяясь на величину
изменяясь на величину 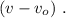
 скорость возрастёт только на величину:
скорость возрастёт только на величину: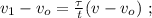
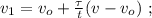

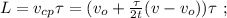 [6]
[6]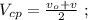
 [7]
[7]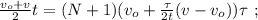
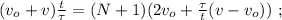
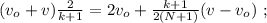


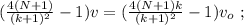
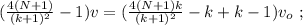


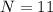 и
и 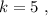 получаем:
получаем: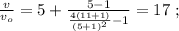
 и
и 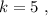 получаем:
получаем: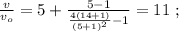
 и
и 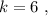 получаем:
получаем: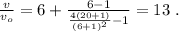
1. задачу можно и нужно решить с закона сохранения импульса
закон сохранения импульса: 0,5*72=(60+0,5)V0,
где V0 –начальная скорость человека.
V0=0,6м/с Ускорение человека будет а=0,05g=0,5м/с^2.
Скорость V=V0-at; V=0,6-0,5t,
найдём время человека в пути,для этого приравняем скорость к нулю.
0=0,6-0,5t; t=1,2с,
тогда путь: S=V0t-at^2/2;
S=0,6*1,2-0,5*1,44/2=1,08м
ответ: S==1,08м
2. задача в прикрепленном файле