связь потенциала и напряженности электрического поля:
E = - (dφ)/(dr)
тогда dφ = - E dr. проинтегрируем полученное выражение:
φ1 - φ2 = ∫E dr.
напряженность поля бесконечного равномерно заряженного проводника:
E = λ/(2 π ε0 r)
φ1 - φ2 = [λ/(2 π ε0)] * ∫dr/r
φ1 - φ2 = [λ/(2 π ε0)] * ln(r2/r1)
φ2 = φ1 - [λ/(2 π ε0)] * ln(r2/r1)
рационально будет для простоты расчетов домножить выражение [λ/(2 π ε0)] на 2. или, впрочем, сразу писать с k
φ2 = φ1 - 2 λ k * ln(r2/r1)
φ2 = 20 - ((2*5*10^(-10))/(9*10^(9)))*1 = 11 В
Дано:
m = 0,1 кг
k = 100 Н/м
A = 8 см = 0,08 м
g = 10 м/с²
Найти:
υ - ?
Воспользуемся законом сохранения энергий, именно при этих формул, мы найдем с какой скоростью груз пружинного маятника:
E(кин.) = E(пот.) - Закон сохранения энергий
E(кин.) =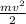 
- Кинетическая энергия влияющая на пружинного маятника
E(пот.) =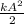 
- Потенциальная энергия влияющая на пружинного маятника
Следовательно:
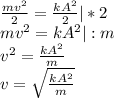- Скорость груза пружинного маятника
υ = √(100 Н/м × (0,08 м)²)/0,1 кг = √(100 Н/м × 0,0064 м²)/0,1 кг = √0,64 (Н×м)/0,1 кг = √0,64 ((кг×м)/с² × м)/0,1 кг = √0,64 ((кг×м²)/с² / 0,1 кг = √6,4 м²/с² ≈ 2,53 м/с
ответ: υ = 2,53 м/с
В общем если воспользоваться 2 законом Ньютона для Батискафа то получим следующее:
Тогда уже из данного соотношения можно отыскать скорость тк:
Предполагаем что при подъеме наверх происходит увеличение кинетической энергии батискафа и так как упоминается о внутренней энергии, то при самом подъеме эта кин энергия и переходит в нагрев батискафа, т.е.: