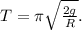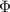 . Угол, на который повернулось колесо (само) относительно состояния в положении равновесия, обозначим
. Угол, на который повернулось колесо (само) относительно состояния в положении равновесия, обозначим 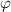 . Радиус кольца -
. Радиус кольца -  , радиус ямы -
, радиус ямы - 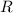 .
.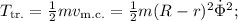
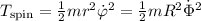
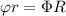 )
)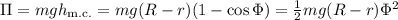
 , а именно, первые два члена разложения косинуса в ряд Тейлора:
, а именно, первые два члена разложения косинуса в ряд Тейлора: 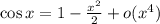 ).
).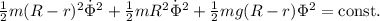
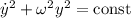 является тем, что в теоретической механике называется первым интегралом уравнения гармонического осциллятора
является тем, что в теоретической механике называется первым интегралом уравнения гармонического осциллятора 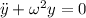 . Омеги, стоящие перед вторыми членами в этих уравнениях в силу некоторых, скорее даже, математических причин, совпадают.
. Омеги, стоящие перед вторыми членами в этих уравнениях в силу некоторых, скорее даже, математических причин, совпадают.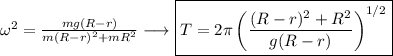
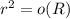 , то есть, что радиус ямы намного больше радиуса кольца. Тогда выражение для периода вырождается в соответствии с предположением (по рабоче-крестьянски, мы тут пренебрегаем квадратом радиуса кольца), в более красивый ответ:
, то есть, что радиус ямы намного больше радиуса кольца. Тогда выражение для периода вырождается в соответствии с предположением (по рабоче-крестьянски, мы тут пренебрегаем квадратом радиуса кольца), в более красивый ответ: