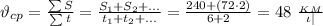
1 в
Объяснение:
Температура однородного медного цилиндрического проводника длинной 10м в течении 57 с повысилась на 10К. Определить напряжение, которое было приложено к проводнику в это время. Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь
L=10 м
t=57 c
∆T= 10 K
U- ?
РЕШЕНИЕ
Количество тепла выделенное проводником по з-ну Дж-Ленца
Q1=U^2/R *t (1)
Сопротивление проводника длиной L
R=λL/S (2)
λ-удельное электрическое сопротивление меди =0.017 Ом*мм2/м=0.017*10^-6 Ом*м
S –поперечное сечение проводника
L-длина проводника
Подставим (2) в (1)
Q1=U^2/( λL/S) *t = U^2*S*t/( λL) (3)
Количество тепла полученное проводником от работы тока
Q2=сm∆T=cVp∆T=cLSp∆T (4)
С-удельная теплоемкость меди =400 Дж/кг*К
m-масса проводника
V-объем проводника
р-плотность меди =8920 кг/м3
по условию задачи потерь тепла нет, тогда
Q1=Q2
Приравняем (3) и (4)
U^2*S*t/( λL)= cLSp∆
U^2 =1/t *( cLp∆T)*( λL)=1/t *c λ p L^2*∆T
U=√(1/t *c λ p L^2*∆T)= √(1/57*400*0.017*10^-6*8920*10^2*10) = 1 В
ответ напряжение 1 В
Составляем уравнение теплового баланса.
Q1=Q2, где первое количество теплоты это то которое получит латунный калориметр и вода после теплообмена с железной гирей (в момент, когда их температура станет одинаковой t), а второе, это сколько отдаст железная гиря.
Q1=c1*m1*(t-t1)+c2*m2*(t-t1)=(c1m1+c2m2)*(t-t1)=Q2=c3m3(t2-t), теперь можно подставить значение чисел и решить уравнение относительно неизвестной, но я предпочитаю выводить формулы. Выводим.
(c1m1+c2m2)*t-t1*(c1m1+c2m2)=c3m3*t2-t*c3m3,>
(c1m1+c2m2)*t+t*c3m3= t1*(c1m1+c2m2)+c3m3*t2, тогда выносим за скобки t
(c1m1+c2m2+c3m3)*t= t1*(c1m1+c2m2)+c3m3*t2
t=(-t1*(c1m1+c2m2)+c3m3*t2)/(c1m1+c2m2+c3m3), t=(15*(380*0,15+4200*0,2)+100*460*0,26)/(380*0,15+4200*0,2+460*0,26)=25415/1016,6=25,таким образом общая установившаяся температура 25 градусов по шкале Цельсия
Объяснение: