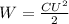, где С - ёмкость конденсатора, U - разность потенциалов на пластинах конденсатора. Из определения напряжённость однородного электрического поля следует , что : 
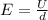,где Е - напряжённость, d- расстояние между пластинами. Ёмкость конденсатора определим по формуле : 
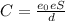, где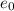 
- электрическая постоянная, е- проницаемость среды( в данном случая она равна 1- т.к конденсатор воздушный), S=π r^2-площадь пластины. Преобразовав все уравнения получим уравнение для энергии конденсатора: 
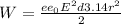. W ≈ (8,854*10^-12 Кл^2/Н*м^2 * 3,14* 0.01^2 м^2*0,005 м 400000^2 В^2/м^2 )/2 ≈1,112*10^-6 Дж.
S = Vx t , где t – полное время полёта, а Vx = Vox, поскольку по горизонтали никакие силы не действуют.
t = 2T , где T – время подъёма и время спуска.
За время подъёма T – вертикальная составляющая начальной скорости будет полностью погашена действием силы тяжести с ускорением свободного падения. А после спуска в самую удалённую точку траектории, через такое же время T отсчитывая от верхней точки траектории – вертикальная составляющая скорости снова возрастёт от нуля до начального значения:
Voy = Tg ;
T = Voy/g ;
t = 2T = 2Voy/g ;
S = Vox t = 2 Vox Voy/g = 2 Vo sinφ Vo cosφ / g = [Vo²/g] 2sinφcosφ ;
S = [Vo²/g] sin2φ ;
Sg/sin2φ = Vo² ;
Vo = √[Sg/sin2φ] ≈ √[56 000 * 9.8 / sin80°] ≈ 747 м/с ;
Для преодоления сопротивления воздуха в полёте на 56 км, снаряду, конечно же, нужно задать намного большую скорость, чем мы рассчитали здесь. Но честный расчёт такой скорости потребовал бы решить систему дифференциальных уравнений, что явно выходит за рамки требований 9-ого класса. ответ для скорости, полученный в данной задаче, соответствует полёту снаряда в вакууме, т.е. в безвоздушном пространстве.