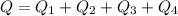
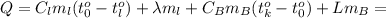
![m_l(C_l[t_0^o-t_l^o]+\lambda)+m_B=](/tpl/images/0668/9467/b5c89.png)
![(C_B[t_k^o-t_0^o]+L]=](/tpl/images/0668/9467/a02e2.png) , т. к.
, т. к. 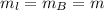 , то
, то![Q=m[(C_l[t_0^o-t_l^o]+\lambda)+(C_B[t_k^o-t_0^o]+L)]=3*](/tpl/images/0668/9467/baca0.png)
![[(2100*[0+10]+340000)+(4200*[100-0]+2300000)]=1540500Dg=](/tpl/images/0668/9467/270ff.png)
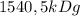
Предлагаю лучшее нормальное решение :з
А С В
∅∅∅
V₀ Vc Vb
ДАНО:
V₀=72 км\ч=20м\с
Vb=0 м/с
1\2 АС = 1\2 АВ
Vc-?
Движение равнозамедленное, значит ускорение на каждом участке пути одинаковое. Исходная формула для ускорения а= (V-V₀) \ 2S.
Весь участок АВ=S, его половина 1\2 АС = 1\2 S
на участке АВ а= (Vb-V₀) \ 2*S
на участке АС а=(Vc-V₀) \ 2*(1\2 S)
приравняем эти выражения: (Vb-V₀) \ 2*S = (Vc-V₀) \ 2*(1\2 S)
преобразуем выражения: Vb - V₀ = 2*(Vc-V₀) = 2*Vc-2*V₀,
отсюда получим 2*Vc= Vb - V₀ + 2*V₀ = Vb + V₀,
Vc= (Vb + V₀) \ 2
подставим известные значения и подсчитаем Vc= 3.5 м\с.
Удачи! :з
Предлагаю лучшее нормальное решение :з
А С В
∅∅∅
V₀ Vc Vb
ДАНО:
V₀=72 км\ч=20м\с
Vb=0 м/с
1\2 АС = 1\2 АВ
Vc-?
Движение равнозамедленное, значит ускорение на каждом участке пути одинаковое. Исходная формула для ускорения а= (V-V₀) \ 2S.
Весь участок АВ=S, его половина 1\2 АС = 1\2 S
на участке АВ а= (Vb-V₀) \ 2*S
на участке АС а=(Vc-V₀) \ 2*(1\2 S)
приравняем эти выражения: (Vb-V₀) \ 2*S = (Vc-V₀) \ 2*(1\2 S)
преобразуем выражения: Vb - V₀ = 2*(Vc-V₀) = 2*Vc-2*V₀,
отсюда получим 2*Vc= Vb - V₀ + 2*V₀ = Vb + V₀,
Vc= (Vb + V₀) \ 2
подставим известные значения и подсчитаем Vc= 3.5 м\с.
Удачи! :з