J = 6,25 кг·м²
m₁ = 50 кг
Объяснение:
Дано:
R = 50 см = 0,50 м
m = 6,4 кг
a = 2 м/с²
_______________
J - ?
m₁ - ?
1)
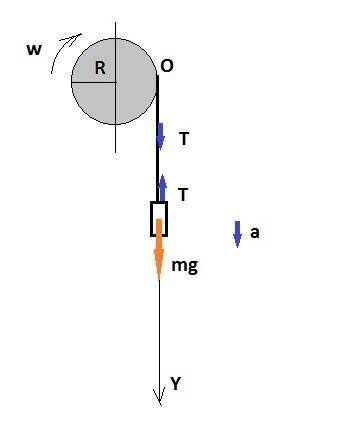
Сделаем чертеж. Ось OY направим вниз.
Составим уравнение для груза. По II закону Ньютона:
ma = mg - T
2)
Натяжение троса - это вес тела, движущегося с ускорением а вниз:
T = P = m·(g - a)
T = 6,4·(9,8-2) ≈ 50 Н
3)
Момент силы:
M = T·R = 50·0,50 = 25 Н·м
4)
Запишем уравнение вращательного движения для вала:
M = J·ε;
ε = a / R = 2 / 0,50 = 4 с⁻²
J = M / ε = 25 / 4 = 6,25 кг·м²
5)
Но момент инерции цилиндра:
J = m₁·R²/2
Тогда:
m₁ = 2·J / R² = 2·6,25 / 0,50² = 50 кг
7,8 км/с
Объяснение:
Дано:
T = 88,85 мин ≈ 5 330 c
h = 230 км = 230*10³ м
R = 6 400 км = 6 400*10³ м
M = 6*10²⁴ кг
G = 6,67*10⁻¹¹ Н*м²/кг
V - ?
1)
Первая космическая скорость:
V₁ = √ (g*R₀), где радиус орбиты
R₀ = (R+h)
2)
Сила притяжения станции к Земле (масса станции m)
F = G*M*m / R₀²
Тогда:
F = G*M*m / (R+h)²
3)
Ускорение свободного падения на этой высоте:
g = F / m = G*M / (R+h)²
4)
V₁ = √ (g*R₀) = √ (G*M / (R+h)) = √ (6,67*10⁻¹¹*6*10²⁴ / (6400+230)*10³) ≈
≈ 7 800 м/с = 7,8 км/с
В этом случае лишнее условие - Т (период вращения)
По формуле
V = 2*π*(R+h)/T = 2*3,14*(6400+230)*10³ / 5330 ≈ 7 800 м/с = 7,8 км/с
Естественно, мы получили тот же самый ответ, но лишними оказались данные о величине массы Земли и гравитационной постоянной.
ТОК меняется от 0,12 А до 0,88 А