Однородная гибкая цепочка длиной l=42 смl=42 см подвешена за свои концы в точках aa и bb так, как показано на рисунке. точка cc – самая нижняя точка цепочки. силы натяжения цепочки в точках aa, bb и cc составляют ta=1,3 нta=1,3 н, tb=1,5 нtb=1,5 н и tc=1,2 нtc=1,2 н соответственно. определите высоту hh между концами цепочки. ответ выразите в см, округлив до целых.

👇

Ответ:

KARAZINO

23.06.2020

Копирую СВОЕ решение из другой задачи и размещаю здесь
************************************************************************
смотри решение во вложениях - два скриншота с выводом формул и один скриншот с результатами для 4-х вариантов

Однородная гибкая цепочка длиной l=42 смl=42 см подвешена за свои концы в точках aa и bb так, как по

Однородная гибкая цепочка длиной l=42 смl=42 см подвешена за свои концы в точках aa и bb так, как по

4,5(36 оценок)

Открыть все ответы

Ответ:

Тимофей225

23.06.2020

ответ:Чтобы вычислить значение КПД указанной наклонной плоскости, воспользуемся формулой: η = Апол / Азатр = m * g * h / (F * l).

Постоянные и переменные: m — масса вытаскиваемого груза (m = 100 кг); — ускорение свободного падения (g ≈ 10 м/с2); h — высота вытаскивания груза (h = 2 м); F — приложенная сила (F = 800 Н); l — длина указанной наклонной плоскости (l = 4 м).

Вычисление: η = m * g * h / (F * l) = 100 * 10 * 2 / (800 * 4) = 0,625 (62,5%).

ответ: КПД указанной наклонной плоскости равен 62,5%.

Объяснение:

4,5(64 оценок)

Ответ:

бооой

23.06.2020

Клевая задача. Максимальная скорость будет в итоге складываться из вертикальной и горизонтальной компонент:
$v= \sqrt{v_y^2+v_x^2}$

Поскольку падение происходит в гравитационном поле, то вертикальная компонента не связана с параметрами капли и зависит только от высоты падения и напряженности поля (ускорения свободного падения), так что с ней все ясно:
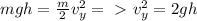
$mgh=\frac{m}{2}v_y^2 =\ \textgreater \ v_y^2=2gh$

Горизонтальная же компонента зависит от силы расталкивания двух частей одной капли. Скорость, приобретенная половинками исходной капли, полностью определит их кинетическую энергию. А по закону сохранения энергии, вся запасенная электростатическая энергия капли разделится между двумя капельками: частично станет их электростатической энергией и частично перейдет в кинетическую (по горизонтальной составляющей скорости). А значит, нам надо найти разность начальной и конечной электростатической энергии. Вот и все.

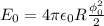
Начальная энергия капли равна $E_0=4\pi\epsilon_0 R\frac{\phi_0^2}{2}$

После разделения капли на две одинаковые их объемчики будут равны половине объема исходной капли, а отсюда находим их радиусы

:
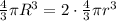
$\frac{4}{3}\pi R^3=2\cdot \frac{4}{3}\pi r^3$
$r=\frac{R}{ \sqrt[3]{2} }$

Энергия распределится поровну, поэтому суммарная электростатическая энергия двух новых капель составит:
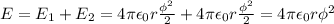
$E=E_1+E_2=4\pi\epsilon_0 r\frac{\phi^2}{2}+4\pi\epsilon_0 r\frac{\phi^2}{2}=4\pi\epsilon_0 r\phi^2$

Потенциал маленькой капли зависит от ее заряда и радиуса. Как изменился радиус мы уже знаем, а вот заряд после разделения распределился пополам - части ведь одинаковые. Поэтому
$\phi=\frac{1}{2}\frac{R}{r}\phi_0= \frac{ \sqrt[3]{2} }{2} \phi_0$

Таким образом, кинетическая энергия, связанная с горизонтальной компонентой скорости, равна
$E_k=\frac{m}{2}v_x^2=E_0-E=4\pi\epsilon_0 R\frac{\phi_0^2}{2}-4\pi\epsilon_0 r\phi^2=4\pi\epsilon_0(R\frac{\phi_0^2}{2}-\frac{R}{ \sqrt[3]{2} }\frac{ (\sqrt[3]{2})^2 }{4}\phi_0^2)$

$E_0-E=4\pi\epsilon_0\phi_0^2R(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})$

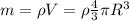$m=\rho V=\rho \frac{4}{3}\pi R^3$ - суммарная масса двух частей, разумеется равна массе исходной капли.

Отсюда
$v_x^2=\frac{2}{\rho \frac{4}{3}\pi R^3}4\pi\epsilon_0\phi_0^2R(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})=\frac{6}{\rho R^2}\epsilon_0\phi_0^2(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})$

$v_x^2=\frac{3\epsilon_0\phi_0^2}{\rho R^2}(1-\frac{\sqrt[3]{2}}{2})$

Окончательно,
$v= \sqrt{v_y^2+v_x^2} = \sqrt{2gh+\frac{3\epsilon_0\phi_0^2}{\rho R^2}(1-\frac{\sqrt[3]{2}}{2})}$