Объяснение:
Решение
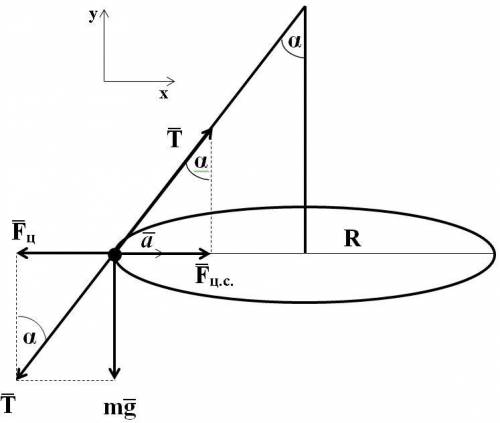
Рисунок прилагается.
Второй закон Ньютона запишем в виде
F(вектор)=m*a(вектор)
где равнодействующая сила
F(вектор)
F(вектор)= m*g(вектор)+T(вектор)
Спроецируем на выбранные оси координат
Y:
T*cos(alpha)-mg=0
T*cos(alpha)=mg
T=mg/cos(alpha)
По условию Гирька весит Р=4,9 Н.
Так как вдоль оси ОУ ускорения равно 0, то по определению Р=m*g
Подставим
T=P/cos(alpha)=4.9/cos30=4.9/0.87=5.66 Н
Эта найденная сила и приводит к тому, что длина шнура меняется.
А величина этого изменения зависит от коэффициента упругости (жесткости) шнура, по закону
T=k*Δl
Отсюда Δl=T/k
k нам не дано, но известно из условий, что Для растяжения шнура на x1=1 см требуется сила F1=6,0 Н. Другими словами F=k*Δx; k=F/Δx=6/0,01=600
Теперь мы знаем k и подставим его
Δl=T/k=5,66/600=0,0094 м
Длина растянутого шнура это l=l0+Δl
Отсюда
l0=l-Δl
l неизвестна. Найдем эту длину.
Заметим что по подобию двух треугольников
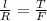
Отсюда l=R*T/F
Так как F действует вдоль ОХ, то нам нужны проекции сил на эту ось
F=T*Sin(alpha)=m*a(центростремительное)
a(центростремительное)=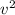
/R
F=T*Sin(alpha)=m*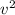/R
Линейная скорость v = w*R
F=T*Sin(alpha)=m*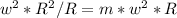
w=2*п*n
F=T*Sin(alpha)=m*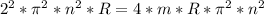
Подставим F в формулу ниже
l=R*T/F=R*T/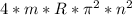
=T/4*m*
,
где m=Р/g
l=T*g/4*P* =0.0716 м
l0=l-Δl=0.0716-0,0094=0,0624 м
l0 нерастянутого резинового шнура = 0,0624 м = 62,4 мм
l растянутого резинового шнура = 0.0716 м = 71,6 мм
неподвижному эскалатору он спускается за 40 секунд. Сколько време-
ни займет спуск идущего пассажира по движущемуся вниз эскалатору?
Дано:
t1 = 60 c
t2 = 40 c
Пусть длина эскалатора l, скорость эскалатора u, ско-
рость человека v.
t3 = ? Когда человек стоит на эскалаторе, который движется
со скоростью u, время его спуска 1
l
t
u = . Если человек со скоростью v идет по
неподвижному эскалатору, он спускается за время 2
v
l
t = .
Когда же человек со скоростью v идет по движущемуся со скоростью u
эскалатору, время его спуска становится равным 3
v
l
t
u = + .
Из первого соотношения:
1
l
u
t = , из второго:
2
v
l
t = . Подставив получен-
ные формулы в выражение для t3, будем иметь:
( )
12 12
3
12 12
1 2
l ltt tt
t l l lt t t t
t t
== = + + +
.
Используя заданныевеличины, получим: 3
60 40 24
60 40
t ⋅ = = +
с.
ответ: 24 с.
2р) Автомобиль проехал вторую половину пути со скоростью в 1,5 раза
большей, чем первую. Определить скорости автомобиля на первой и второй
половинах пути в км/час, если средняя скорость автомобиля на всем пути
равна vср = 30 км/час.
Дано:
v2 = 1,5 v1
vср = 30 км/ч
По определению средней скорости ср
д
v
S
t = , где tд –
время, за которое материальная точка проходит путь S.
Исходя из введенных обозначений, здесь д 1 2 t tt = + .
v1 – ?
v2 – ?
Время, за которое автомобиль проходит первую половину пу
ответ: A=10 кДж