Дано:
h = 5 м
S = 10 м
v₀ = 0
μ = 0.2
t - ?
v - ?
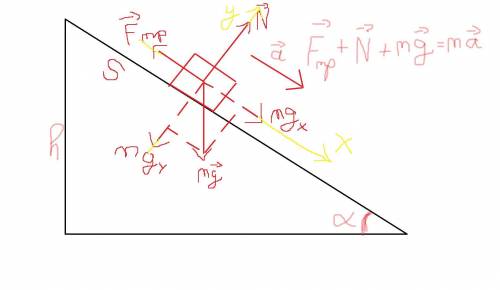
Силы, действующие на тело: сила трения, реакции опоры и тяжести.
Fтр, N, mg соответственно (направления сил на рисунке).
Запишем второй закон Ньютона для тела:
Fтр + N + mg = ma (сумма векторная, как на рисунке).
В проекции на ось X:
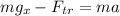
В проекции на ось Y:
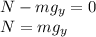
Выразим mgx и mgy через mg и угол α:
mgx = mgsinα
mgy = mgcosα
Найдём sinα и cosα.
sinα = h / S = 5 / 10 = 0.5
Значит α = 30°
cosα = cos30° = √3 / 2 ≈ 0.866
По формуле, Fтр = μN, N = mgy = mgcosα => Fтр = μmgcosα
Перепишем проекцию на X с новым значением Fтр и найдём a:
mgsinα - μmgcosα = ma
gsinα - μgcosα = a
a = g(sinα - μcosα)
По формуле динамики, S = v₀t + at² / 2. v₀ = 0 по условию, => S = at²/2.
Отсюда t = √(2S / a) = √(2S / g(sinα - μcosα))
Опять по формуле динамики:
=> 
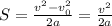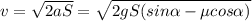
Конечные формулы:
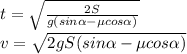
≈ 2,5 с
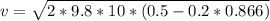≈ 8 м/с
Температура 373 К = 100 °С, а это температура кипения воды. Следовательно, чтобы пар, взятый при температуре кипения, превратить в лед при температуре tк = –10 °С, необходимо четыре процесса:
1) сконденсировать пар в воду при температуре t0 = 100 °C, при этом выделится количество теплоты Q1 = m⋅L, где L = 2,3⋅106 Дж/кг — удельная теплота парообразования воды (табличная величина);
2) охладить воду от t0 = 100 °C до t1 = 0 °C (температура замерзания воды), при этом выделится Q2 = c1⋅m⋅(t0 – t1), где c1 = 4,19⋅103 Дж/(кг⋅К) — удельная теплоемкость воды (табличная величина);
3) заморозить воду в лед при температуре t1 = 0 °C, при этом выделится Q3 = m⋅λ, где λ = 330⋅103 Дж/кг — удельная теплота плавления льда (табличная величина);
4) охладить лед от t1 = 0 °C до tк = –10 °C, при этом выделится Q2 = c2⋅m⋅(t1 – tк), где c2 = 2,1⋅103 Дж/(кг⋅К) — удельная теплоемкость льда (табличная величина).
Всего пар отдаст количество теплоты, равное
Q = Q1 + Q2 + Q3 + Q4 = m⋅(L + c1⋅(t0 – t1) + λ + c2⋅(t1 – tк)),
Q = 9,2⋅10^6 Дж.
U=12.5 I=12.5/50-0.25А
R=50 ответ:0.25А
Найти I