Физика: Период и частота механических колебаний

Период и частота механических колебаний

👇

Ответ:

АрзуНаз

01.06.2022

1) Период колебаний-это время совершения одного колебания, определяется по формуле:
T=t/n
Где t-время, n-число колебаний.
Единица измерения секунда-с

2) Частота колебаний-это число колебаний, совершаемых за единицу времени, определяется по формуле:
ν=n/t
Единица измерения секунда в минус первой степени-с⁻¹, или герц-Гц.

3) Частота и период обратны друг другу:
T=1/ν ; ν=1/T

4,8(15 оценок)

Открыть все ответы

Ответ:

Maciel

01.06.2022

Попытаюсь решить.

1. Сразу ясно, что частица находится в параболической потенциальной яме, в таких условиях она является гармоническим осциллятором.

Функция Лагранжа для такой частицы

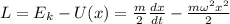
$L=E_k-U(x)=\frac{m}{2}\frac{dx}{dt}-\frac{m\omega ^2x^2}{2}$

Уравнение Эйлера-Лагранжа

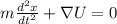
$m\frac{d^2x}{dt^2}+\nabla U=0$

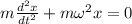
$m\frac{d^2x}{dt^2}+m\omega^2x=0$

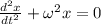$\frac{d^2x}{dt^2}+\omega^2x=0$ - классическое уравнение гармонического осциллятора, о чем было сказано в начале.

Его общее решение

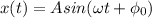
$x(t)=Asin(\omega t+\phi_0)$

Решим задачу Коши для указанных условий (примем начальную фазу для простоты за ноль)

1) Начальное положение частицы - положение равновесия, но есть отличная от нуля начальная скорость 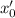x_0'

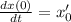
$\frac{dx(0)}{dt} =x_0'$

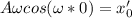
$A\omega cos(\omega *0)=x'_0$

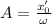
$A=\frac{x_0'}{\omega}$

Частное решение 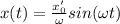$x(t)=\frac{x_0'}{\omega}sin(\omega t)$

2) Здесь наоборот, частица выведена из положения равновесия, но не имеет начальной скорости, значит амплитуда сходу будет равна 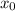x_0 , а частное решение будет иметь вид

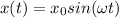
$x(t)=x_0sin(\omega t)$

2) Момент инерции вычисляется как интеграл следующего вида

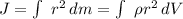
$J=\int\ {r^2} \, dm=\int\ {\rho r^2} \, dV$

Где dV - объем цилиндрического коаксиального слоя толщиной dr

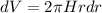
$dV=2\pi Hrdr$

Окончательно

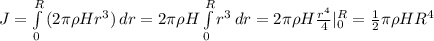
$J=\int\limits^R_0 {(2\pi\rho Hr^3)} \, dr= 2\pi \rho H \int\limits^R_0 {r^3} \, dr =2\pi \rho H \frac{r^4}{4}|_0^R=\frac{1}{2}\pi \rho HR^4$

Центростремительное ускорение по внешнему радиусу тора должно совпасть с g₀

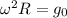
$\omega ^2R=g_0$

Требуемая угловая частота вращения

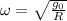
$\omega=\sqrt{\frac{g_0}{R} }$

Период обращения

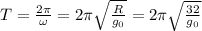
$T=\frac{2\pi }{\omega} =2\pi \sqrt{\frac{R}{g_0} }=2\pi \sqrt{\frac{32}{g_0} }$

Частота обращения

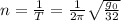$n=\frac{1}{T}=\frac{1}{2\pi } \sqrt{\frac{g_0}{32} }$ .

4,4(99 оценок)

Ответ:

гуля429

01.06.2022

На полюсе 9,82 Н

на экваторе 9,79 Н

Примечание: Мои результаты несколько отличаются от фактических (9,83 и 9,78 соответственно) потому-что Земля была принята в расчетах за шар, а не за геоид.

Объяснение:

Вычислим сначала "чистое" ускорение свободного падения, рассмотрев землю как неподвижный шар, это, кстати, совпадет со значением ускорения свободного падения на полюсах.

Сила тяжести сообщает телу ускорение свободного падения, запишем второй закон Ньютона

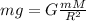
$mg=G\frac{mM}{R^2}$

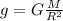
$g=G\frac{M}{R^2}$

Масса Земли М=5,972*10²⁴ кг, а радиус (да, земля геоид, пренебрежем этим) R=6,371*10⁶ м.

Тогда, ускорение свободного падения на полюсе

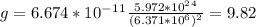$g=6.674*10^-^1^1\frac{5.972*10^2^4}{(6.371*10^6)^2}=9.82$ м/с²

На экваторе, кроме силы тяжести, возникает фиктивная сила инерции, обусловленная суточным вращением Земли и ускорение свободного падения уменьшится на величину центростремительного ускорения

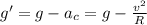
$g'=g-a_c=g-\frac{v^2}{R}$

Скорость вращения точек экватора легко найти

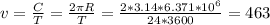$v=\frac{C}{T}=\frac{2\pi R}{T} =\frac{2*3.14*6.371*10^6}{24*3600}=463$ м/с

Значит, ускорение свободного падения на экваторе

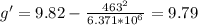$g'=9.82-\frac{463^2}{6.371*10^6} =9.79$ м/с²

Осталось самое простое - посчитать вес тела массой 1 кг. Фактически он будет принимать те же числовые значения, что и ускорения. На полюсе тело массой 1 кг будет весить 9,82 Н, а на экваторе 9,79 Н.

4,4(17 оценок)

Это интересно:

Стиль-и-уход-за-собой

17.12.2021

Горячее масло: идеальный способ привести ваши волосы в порядок?...

Компьютеры-и-электроника

10.11.2021

Как изменить список программ для автозапуска...

Кулинария-и-гостеприимство

31.12.2020

Как приготовить пасту Чикен Альфредо, чтобы она получилась вкусной?...

Дом-и-сад