Дано:
m(ч)=60 кг
m(л)=40 кг
V=0
V(ч)₁=4 м/с
-------------------
V(л)₁-?
Задачу можно решить 2-мя через третий закон Ньютона и через импульсы.
импульсы):
p=(m(ч) + m(л))*V
p=m(ч)*V(ч)₁ + m(л)*V(л)₁
Если равны левые части, то можно и приравнять правые:
(m(ч) + m(л))*V =m(ч)*V(ч)₁ + m(л)*V(л)₁
Поскольку V=0, то уравнение будет виду:
m(ч)*V(ч)₁ + m(л)*V(л)₁ = 0
m(л)*V(л)₁ = -m(ч)*V(ч)₁
V(л)₁ = -m(ч)*V(ч)₁ / m(л) - минуса не пугаемся - это всего лишь направление.
Подставляем числа :
V(л)₁ = -60*4 / 40
V(л)₁ = -6 (м/с)
закон Ньютона):
Запишем 3 закон Ньютона:
F(л) = -F(ч)
m(л)*a(л) = -m(ч)*a(ч)
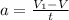
m(л)*(V(л)₁-V)/t = -m(ч)*(V(ч)₁-V)/t
Сокращаем время:
m(л)*(V(л)₁-V) = -m(ч)*(V(ч)₁-V)
Открываем скобки учитывая, что V=0
m(л)*V(л)₁ = -m(ч)*V(ч)₁
V(л)₁ = -m(ч)*V(ч)₁/m(л)
Подставляем числа :
V(л)₁ = -60*4 / 40
V(л)₁ = -6 (м/с)
ответ: 6 м/с.
максимальный груз, который может поднять подъёмно кран, составляет m = 2449 кг.
Объяснение:
Задать во Войти
АнонимФизика21 мая 21:58
Мотор подъемного крана мощностью 1,5 кВт поднимает груз со скоростью 3м/мин. Какой максимальный груз может поднимать
он при данной скорости, если его кпд = 80 %?
РЕКЛАМА
ответ или решение1
Сазонова Дарья
N = 1,5 кВт = 1500 Вт.
V = 3 м/мин = 0,05 м/с.
g = 9,8 м/с2.
КПД = 80 %.
m - ?
Согласно определению, КПД определяется формулой: КПД = Апол * 100 % / Азат, где Апол - полезная работа, Азат - затраченная работа.
Затраченную работу Азат выразим формулой: Азт = N * t, где N - мощность мотора подъёмного крана, t - время его работы.
Полезную работу Апол выразим по формуле: Апол = m * g * h.
КПД = m * g * h * 100 % / N * t.
Отношение высоты подъёма h к времени подъёма t будет скоростью поднимания груза V: V = h / t.
КПД = m * g * V * 100 % / N.
m = КПД * N / g * V * 100 %.
m = 80 % * 1500 Вт / 9,8 м/с» * 0,05 м/с * 100 % = 2449 кг.
Видимая поверхность солнца