Дано:
\(L=300\) м, \(S_1=2t+2,5t^2\), \(S_2=3t\), \(S_1(\tau)-?\)
Решение задачи:
Если тела движутся из двух разных точек A и B, причем навстречу друг другу, то сумма пройденных ими путей за время \(\tau\) до встречи равна расстоянию между этими точками \(L\), то есть:
S1(τ)+S2(τ)=L 2τ+2,5τ2+3τ=300 Решим это квадратное уравнение для нахождения времени до встречи: 2,5τ2+5τ–300=0 τ2+2τ–120=0 D=4+4⋅120=484 τ=–2±222 [τ=–12сτ=10с
Время не может быть отрицательным, поэтому откидываем первый корень. Для того, чтобы найти S1(τ) подставим найденное время в уравнение движения первого тела. S1(10)=2⋅10+2,5⋅102=270м ответ: 270 м.
Объяснение:
Дано:
ρв. = 1000 кг/м^3
ρм. = 800 кг/м^3
ρр. = 13600 кг/м^3
h = 5 см = 0.05 м
H = 7.5 см = 0.075 м
---------------------------------
роб. - ?
p' - ?
Мы знаем то, что наиболее плотная жидкость будет находиться на ниже, чем менее плотная жидкость.
Отсюда
( см. рисунок )
роб. = рв. + рм. + рр.
роб. = ρв.gh + ρм.gh + ρ.pgh
роб. = gh( ρв. + ρм. + ρ.p )
pоб. = 10 * 0.05( 1000 + 890 + 13600 ) = 7,7 кПа
( см. рисунок )
h' = H - h
h' = 7.5 - 5 = 2.5 см = 0.025 м
p' = рм. + рв.'
p' = ρм.gh + ρв.gh'
p' = g( ρм.h + ρв.h' )
p' = 10( 800 * 0.05 + 1000 * 0.025 ) = 650 Па
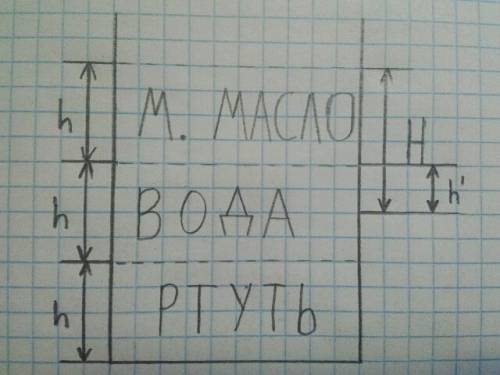
б) свеча находится в двойном фокусе
в) свеча находится между двойным фокусом и фокусом