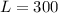 м, длину поезда l, скорость нашего поезда
м, длину поезда l, скорость нашего поезда 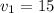 м/с, скорость второго поезда
м/с, скорость второго поезда 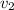 , время проезда через туннель
, время проезда через туннель 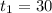 сек, а скорость проезда мимо поезда
сек, а скорость проезда мимо поезда 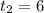 сек. Тогда
сек. Тогда 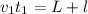 , оттуда
, оттуда 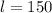 м. Теперь второй случай, поезд мимо поезда
м. Теперь второй случай, поезд мимо поезда 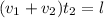 ,
, 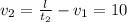 м/с. Второй поезд ехал со скорость 10 метров в секунду.
м/с. Второй поезд ехал со скорость 10 метров в секунду.