Рассмотрим два случая.
1. На шарик действует лишь сила со стороны электрического поля, а сила тяжести не действует.
Силу рассчитаем, как произведение эл. заряда на напряженность поля:
F = Eq
Далее найдем ускорение, с которым этот шарик двигался бы в электрическом поле, не будь он подвешен на нити:
а = F/m (по второму закону Ньютона)
Теперь воспользуемся формулой для определения периода колебаний нитяного маятника в однородном гравитационном поле:
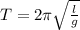
Только вместо ускорения свободного падения g, используем ускорение a, рассчитанное нами ранее. Получим формулу:
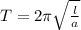или с учетом ранее проведенных выкладок:
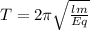
Здесь, напоминаю, l - длина нити
Расчёт: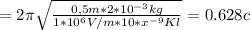 
2. Если на тело действует дополнительно сила тяжести, сообщающая ему ускорение свободного падения g = 9,8 м/с². Всё то же самое, только вместо ускорения a в формуле будет ускорение (a+g)
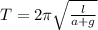
Здесь удобнее a рассчитать отдельно:
a = Eq/m = 1*10⁶В/м ˣ 10*10⁻⁹ Кл / 0,002 кг = 5 м/с²
Тогда a+g = 9,8 м/с² + 5 м/с² = 14,8 м/с²
А при расчете период колебаний получим
Вечный двигатель первого рода
Вечный двигатель, перпетуум-мобиле— воображаемая машина, которая, будучи раз пущена в ход, совершала бы работу неограниченно долгое время, не заимствуя энергии извне. Возможность работы такой машины неограниченное время означала бы получение энергии из ничего.
Идея вечного двигателя возникла в Европе, по-видимому, в XIII веке (хотя существуют свидетельства, что первый проект вечного двигателя предложил индиец Бхаскара в XII веке). До этого проекты вечных двигателей неизвестны. Их не было у греков и римлян, которые разработали множество эффективных механизмов и заложили основы научных подходов к изучению природы. Ученые предполагают, что дешевая и практически неограниченная рабочая сила в виде рабов тормозила в античности разработку дешевых источников энергии.
1) Координаты векторов а=АВ и в=СД
Определение вектора:
Если даны две точки плоскости А (х1;у1) и В (х2;у2), то вектор АВ имеет следующие координаты: АВ (х2-х1;у2-у1)
а=АВ=(9-9;6-10)=(0;-4)
в=СД=(3-6;2-2)=(-3;0)
2) Длина (модуль) векторов АВ и СД
Длина обозначается знаком модуля.
Если даны две точки плоскости А (х1;у1) и В (х2;у2), то длину отрезка а=АВ можно вычислить по формуле:
|а|=|АВ|=√((х2-х1)^2+(у2-у1)^2)=√((9-9)^2+(6-10)^2)=√(0+(-4)^2)=√16=4;
|в|=|СД|=√((х4-х3)^2+(у4-у3)^2)=√((3-6)^2+(2-2)^2)=√(-3^2+0=3;
3) Построить векторы а и в на координатной плоскости и построить вектор м=а+в
Вектор а и вектор в перенесём на плоскости ХОУ началами в точку О (0;0). Далее см. рисунок;
На векторах а и в строим вектор м=а+в (жёлтый)
4) Найти координаты вектора м и его длину
Координаты вектора м равны: хм=ха+хв=0-3=-3; ум=уа+ув=-4+0=-4; м (-3;-4);
Длина вектора м (-3;-4) равна √((-3)^2+(-4)^2)=√(9+16=√25=5;
5) Построить векторы АВ и СД на координатной плоскости и построить вектор н=а-в
Тот же рисунок, но добавляем вектор, равный минус вектор СВ
(той же длины, но в противоположную сторону направленный)
На векторах а и -в строим вектор н=а-в (зелёный)
6) Найти координаты вектора н и его длину
Координаты вектора н равны: хн=ха-хв=0+3=3; ун=уа+ув=-4+0=-4; н (3;-4);
Длина вектора н (3;-4) равна √((+3)^2+(-4)^2)=√(9+16=√25=5;
7) Найти координаты вектора д=2а-в и его длину
Строим вектор 2а. (из точки О, но в 2 раза длиннее, чем а, пунктиром красным жирным)
Чуток сместим его для наглядности.
На векторах 2а и -в строим вектор д=2а-в (зелёный пунктир)
8) Найти скалярное произведение векторов а и в
Определение: Скалярным произведением двух векторов а и в называется ЧИСЛО,
равное произведению длин этих векторов на косинус угла между ними: а*в=|а|*|в|*cos(а; в) ;
Из 2) имеем: |а|=4; |в|=3; угол между ними равен 90 градусов (Пи/2): cos(Пи/2)=0.
Откуда а*в=|а|*|в|*cos(а; в) =4*3*0=0;
9) Найти величину силы F, совершившей работу А по перемещению тела
из точки С в точку D А=F*S; F=А/S; S есть длина вектора СД и, как вычислено в 2), S=3.
Откуда F=30/3=10.