Question

Решить по : гладкое металлическое тело можно бросить под углом 45° или с той же скоростью пустить скользить по льду при коэффиценте трения 0,02. в каком случае тело окажется дальше от места бросания? сопротивлением воздуха пренебречь.

Answer 1

Рассмотрим эти два движения по отдельности:

1. Законы движения тела по осям x, y:

$x = v_x t$

$y = v_y t - \frac{gt^2}{2}$

Так как угол = 45, то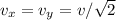 $v_x = v_y = v/\sqrt{2}$

Падение будет там, где y=0, обозначим время падения как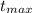 $t_{max}$, тогда оно будет равно:

$t_{max} = \frac{\sqrt{2}v}{g}$

Подставим это в формулу для координаты x, найдем дистанцию броска.

$x_{max} = \frac{v}{\sqrt{2}}t_{max} = \frac{v^2}{g}$

2. Закон движения по оси x (по другой оси движения нет):

$x = vt - \frac{at^2}{2}$

Ускорение найдем из второго закона Ньютона:

$ma = F = \mu N = \mu mg$, так как действующая на тело сила по оси x это сила трения, равная μN.

Чтобы найти точку остановки вспомним, что движение является равнозамедленным и в конечной точке скорость = 0. Скорость же выражается так:

$v(t) =v -at$

Тогда время на бросок:

$t_{max} = \frac{v}{a} = \frac{v}{\mu g}$

Подставляя в формулу для координаты x, получим:

$x_{max} = vt_{max} - \frac{at_{max}}{2} = \frac{v^2}{\mu g} - \frac{v^2}{2\mu g} = \frac{v^2}{2\mu g} = \frac{v^2}{0,04 g}$

Итого, сравнивая расстояние 1 и расстояние 2, заключаем, что во втором случае тело пролетит гораздо дальше.