Объёмы горячей и холодной воды: V₁ = V₂ = V = 3 л = 3 * 10⁻³ м³.
Температура горячей воды (кипения воды): t₁ = 100 °C.
Температура холодной воды: t₂ = 15 °C.
Найти изменение температуры горячей воды Δt₁ - ?Решение:0. Тепло, полученное от остывания кипятка тратится на нагревание холодной воды. В итоге устанавливается общая температура t.
1. Сразу найдём массу воды: m₁ = m₂ = m = ρV = 1000 * 3 * 10⁻³ = 3 (кг) (на самом деле она нам нужна, почему - узнаете далее).
2. Запишем уравнение теплового баланса: cm(t₁ - t) = cm(t - t₂).
3. Сократим на c и m и (огого!) масса нам больше не нужна: t₁ - t = t - t₂.
4. Выразим общую конечную температуру:
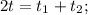
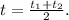
5. Тогда изменение температуры горячей воды:

 (°C).
(°C).
R₂/R₁=√2.
Объяснение:
Запишем для мощности P, Вт на сопротивлении R₁ до замыкания ключа:
P=I²*R₁; I=U/R₁₂;
P=R₁*(U/R₁₂)², где
R₁₂ - эквивалентное сопротивление цепи, Ом до замыкания ключа:
для мощности P', Вт на сопротивлении R₁ после замыкания ключа:
P'=R₁*(U/R₁₂₂)², где
R₁₂₂ - эквивалентное сопротивление цепи, Ом после замыкания ключа:
По условию:
P'/P=2;
P'/P=R₁*(U/R₁₂₂)²/R₁*(U/R₁₂)²=R²₁₂/R²₁₂₂;=2;
R₁₂/R₁₂₂=√2.
Вычислим эквивалентные сопротивления до и после замыкания ключа:
R₁₂=R₁+R₂;
R₁₂₂=R₁+R₂*R₂/(R₂+R₂)=R₁+R₂/2.
Подставим и решаем:
(R₁+R₂)/(R₁+R₂/2)=√2;
R₁+R₂=√2(R₁+R₂/2);
R₁+R₂=√2R₁+√2R₂/2;
R₁+R₂-√2R₁-√2R₂/2=0;
Разделим все на R₁:
R₁/R₁+R₂/R₁-√2R₁/R₁-√2R₂/(2R₁)=0;
1+R₂/R₁-√2-√2R₂/(2R₁)=0;
R₂/R₁(1-√2/2)+1-√2=0;
немного алгебры:
R₂/R₁=(√2-1)/(1-√2/2)=2(√2-1)/(2-√2)=2(√2-1)/(√2(√2-1))=
=2/√2=2√2/2=√2
R₂/R₁=√2.
Проверим. Пусть R₁=1 Ом или относительных единиц, тогда R₂=√2;
R₁₂=1+√2;
R₁₂₂=1+√2/2;
R²₁₂/R²₁₂₂=(1+√2)²/(1+√2/2)²=(1+2√2+2)/(1+√2+1/2)=(3+2√2)/(3/2+√2)=2*(3+2√2)/(3+2√2)=2