Обозначения:
V - объём
p - давление;
T - абсолютная температура (по шкале Кельвина)
t - температура (по шкале Цельсия)
k - постоянная Больцмана
R - универсальная газовая постоянная
N - количество молекул в веществе
M(E) - молярная масса атома/молекулы
υ(кв) - средняя квадратичная скорость движения молекул
ρ - плотность вещества
Nₐ - постоянное число Авогадро
m₀ - масса одной молекулы
n - концентрация молекул
Wк - средняя кинетическая энергия поступательного движения молекулы
1) Дано: V = 1 см³ = 10⁻⁶ м³; p = 4,14 × 10⁻¹⁰ Па; T = 300 К; k = 1,38 × 10⁻²³ Дж/К
Найти: N - ?
Решение. Количество молекул в газе можно найти через закон Авогадро: в равных объёмах газов при одинаковых температур и давления содержится одинаковое количество молекул: N = pV/kT
Найдём значение искомой величины:
[N] = Па×м³×К/Дж×К = Па×м³/Дж = Н×м³/Дж×м² = Н×м/Дж = Дж/Дж = 1
N = 4,14 × 10⁻¹⁰ × 10⁻⁶/1,38 × 10⁻²³ × 300 = 10⁷/100 = 10⁵ Па = 100000 Па
ответ: 100000.
2) Дано: при t = 0 °С ⇒ Т = 273,15 К; р = 10⁵ Па; R = 8,31 Дж/К × моль; M(H₂) = 2Ar(H) = 2 × 1 = 2 г/моль = 2 × 10⁻³ кг/моль
Найти: υ(кв) - ?
Решение. Из определения кинетической энергии Wк = m₀υ²/2 и формулы связи кинетической энергии и абсолютной температуры Wк = 3kT/2 можно получить формулу для расчёта средней квадратичной скорости (υ(кв)) поступательного движения молекул идеального газа:
m₀υ²/2 = 3kT/2 ⇒ υ² = 3kT/m₀, где υ(кв) = √(υ²) ⇒ υ(кв) = √(3kT/m₀)
Так как нам неизвестно m₀, найдём её по формуле: m₀ = M(H₂)/Nₐ и получим: υ(кв) = √(3kNₐT/M(H₂)), где k × Nₐ = R:
υ(кв) = √(3RT/M(H₂))
Найдём значение искомой величины:
[υ(кв)] = √(Дж×К×моль/К×моль×кг) = √(Дж/кг) = √(Н×м/кг) = √(кг×м×м/кг×с²) = √(м²/с²) = м/с
υ(кв) = √(3×8,31×273,15/2×10⁻³) = √(6809,6295/2×10⁻³) = √(3404814,75) ≈ 1845 м/с = 1,845 км/с
ответ: 1,8.
3) Дано: при t = 27 °С ⇒ Т = 300,15 К; ρ = 0,29 кг/м³; R = 8,31 Дж/К × моль; M(H₂О) = 2Ar(H₂) + Ar(O) = 2 × 1 + 16 = 18 г/моль = 18 × 10⁻³ кг/моль.
Найти: р - ?
Решение. Из основного уравнения молекулярно-кинетической теории (МКТ) можно выразить зависимость давление гага (р) от концентрации молекул (n) и абсолютной температуры (T): р = 2nWк/3, где Wк = 3kT/2 ⇒ р = nkT, где n = ρ/m₀ = ρNₐ/M(H₂О);
Значит, p = ρkNₐT/M(H₂О), где k × Nₐ = R:
p = ρRT/M(H₂О)
Найдём значение искомой величины:
[p] = кг×Дж×К×моль/м³×К×моль×кг = Дж/м³ = Н×м/м³ = Н/м² = Па
p = 0,29×8,31×300,15/18×10⁻³ = 723,331485/18×10⁻³ = 723331,485/18 = 40185,0825 Па = 40,1850825 кПа
ответ: 40.
17.1. в закрытом медном колориметре массой m1 = 0,2 кг находится лед массой m2 = 1 кг при температуре −10 °с. в колориметр впускают пар массой m3 = 0,2 кг, имеющий температуру 110 °с. какая температура установится в колориметре? удельную теплоемкость паров воды в интервале от 100 до 110 °с считать равной 1,7 кдж/(кг•к). удельная теплота парообразования воды равна 2,1 мдж/кг, удельная теплота плавления льда 0,34 мдж/кг. [37 °с]
17.2. при соблюдении необходимых предосторожностей вода может быть переохлаждена до температуры −10 °с. сколько льда образуется из такой воды массой 1 кг, если в нее бросить кусочек льда и этим вызвать замерзание воды? какую температуру должна иметь переохлажденная вода, чтобы она целиком превратилась в лед? удельная теплоемкость переохлажденной воды 4,19 кдж/(кг•к), льда 2,1 кдж/(кг•к). удельная теплота плавления льда 0,33 мдж/кг. [0,12 кг; −160 °с]
17.3. в колбе находилась вода при 0 °с. выкачиванием из колбы воздуха заморозили всю воду в сосуде. какая часть воды при этом испарилась, если колба была теплоизолирована? удельная теплота испарения воды 2,5 мдж/кг. удельная теплота плавления льда 0,33 мдж/кг. [11,7 %]
17.4. в дьюаровском сосуде, содержащем жидкий азот при температуре −195 °с, за время 24 ч испаряется азот объемом 10−3м3 при температуре окружающего воздуха 20 °с. определите удельную теплоту парообразования азота, если известно, что при температуре 0 °с в том же сосуде за время 22,5 ч тает лед массой 4•10−3 кг. считать, что количество теплоты, подводимое ежесекундно к сосуду, пропорционально разности температур снаружи и внутри сосуда. плотность жидкого азота 800 кг/м3, удельная теплота плавления льда 0,33 мдж/кг. [0,019 мдж/кг]
17.5. лед массой 1 кг при температуре 0 °с заключен в теплонепроницаемый сосуд и подвергнут давлению 6,9•107 па. сколько льда расплавится, если при увеличении давления на δp = 3,8•107 па температура плавления льда понижается на 1 °с? понижение температуры плавления от 0 °с считать пропорциональным увеличению давления сверх атмосферного. [11,3 г]
17.6. некоторая установка, развивающая мощность 30 квт, охлаждается проточной водой, текущей по спиральной трубке сечением 1 см2. при установившемся режиме проточная вода нагревается на 15 °с. определите скорость воды, предполагая, что на нагревание воды идет η = 0,3 мощности, развиваемой установкой. [1,44 м/с]
17.7. санки массой 5 кг скатываются с горы, которая образует с горизонтом 30°. пройдя расстояние 50 м, санки развивают скорость 4,1 м/с. вычислите количество теплоты, выделенное при трении полозьев о снег. [1,19 кдж]
17.8. свинцовая пуля, летящая со скоростью 400 м/с, попадает в стальную плиту и отскакивает от нее со скоростью 300 м/с. какая часть пули расплавится, если ее температура в момент удара была равна 107 °с и на нагревание пули пошло η = 0,8 всей работы, совершаемой при ударе? удельная теплоемкость и удельная теплота плавления свинца равны соответственно 126 дж/(кг•к), 25 кдж/кг. [0,05]
Давление идеального газа рассчитывается по формуле: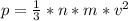
. Для данного электронного газа имеем: 
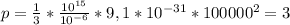паскаля.
Чтобы давление было в паскалях (единица измерения давления в СИ), кубический сантиметр выразил как десять в минус шестой степени кубометров. А скорость выразил в м/с, доумножив 100 на 1000.
ответ: 3 Па.