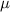 . На этом кубе вплотную к нему сверху расположен клин массой
. На этом кубе вплотную к нему сверху расположен клин массой 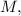 с углом наклона к поверхности куба
с углом наклона к поверхности куба 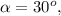 который без трения может двигаться по кубу. Поперечно к подстилающей поверхности движется шар, сталкивающийся с клином. Взаимодействие трёх тел далее считаем упругим. Для простоты решения начальный импульс будет считать проходящим через центр масс системы трёх тел, так чтобы не было момента импульса и дополнительных неизвестных в виде угловых скоростей этих тел.
который без трения может двигаться по кубу. Поперечно к подстилающей поверхности движется шар, сталкивающийся с клином. Взаимодействие трёх тел далее считаем упругим. Для простоты решения начальный импульс будет считать проходящим через центр масс системы трёх тел, так чтобы не было момента импульса и дополнительных неизвестных в виде угловых скоростей этих тел.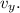
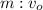 – до соударения направлена вниз, после соударения
– до соударения направлена вниз, после соударения  – от клина по горизонтали; и вверх по вертикали
– от клина по горизонтали; и вверх по вертикали 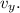 Скорость клина
Скорость клина 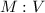 – после соударения от шара по горизонтали; и вверх от куба по вертикали
– после соударения от шара по горизонтали; и вверх от куба по вертикали 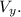 Скорость куба
Скорость куба 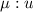 – после соударения направлена вниз. Итак, у нас имеется 5 неизвестных. Для них мы сможем составить 4 уравнения и поколдовать над ними в предельном случае, когда
– после соударения направлена вниз. Итак, у нас имеется 5 неизвестных. Для них мы сможем составить 4 уравнения и поколдовать над ними в предельном случае, когда 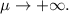
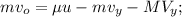 ЗСИ по вертикали.
ЗСИ по вертикали.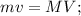 ЗСИ по горизонтали.
ЗСИ по горизонтали.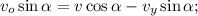 неизменность продольной составляющей
неизменность продольной составляющей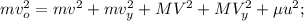 ЗСЭ
ЗСЭ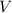 и
и 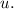
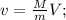
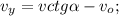
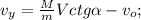
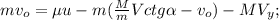
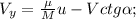
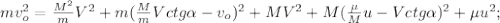
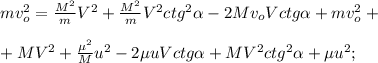
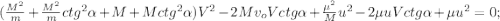
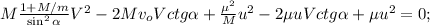
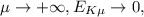
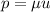 – остаётся конечным!
– остаётся конечным!![M \frac{ 1 + M/m }{ \sin^2{ \alpha } } [V]^2 - 2 M v_o ctg{ \alpha } [V] + \frac{1}{M}[p]^2 - 2 ctg{ \alpha } [p] [V] = 0 ;](/tpl/images/0679/8109/f0f8e.png)
 проходящего через начало координат, а стало быть при различных значениях
проходящего через начало координат, а стало быть при различных значениях 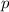 мы будем получать различные значения
мы будем получать различные значения 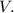 Т.е. предположение о том, что при любом значении параметра
Т.е. предположение о том, что при любом значении параметра 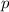 – находилось бы фиксированное решение квадратного уравнения
– находилось бы фиксированное решение квадратного уравнения 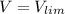 , не верно.
, не верно.




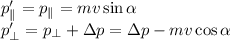
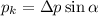
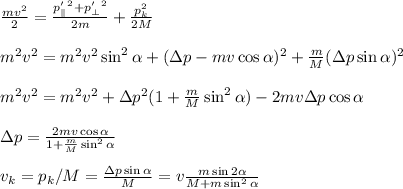
V=s/t
V=600/900=6/9
t2=Vs
t2=6/9*6000/1 записываем дробями решаем
и получаем 400 сек