А 18. 4
А 19. 2
Объяснение:
Без паники.
А 18. Первоначальное значение силы натяжения нити совпадает с весом шарика
Н
После помещения второго заряженного шарика под первый, между ними возникает сила кулоновского притяжения и натяжение нити увеличивается, величина это кулоновской силы
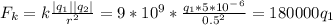Н
Новое натяжение нити
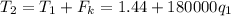Н
но оно в два раза больше прежнего, значит составляем уравнение
Кл или 8 мкКл.
А 19. Потенциальная энергия заряда в поле другого заряда
Выходит, потенциальная энергия обратно пропорциональная расстоянию. Посмотрим, во сколько раз увеличилось расстояние, было 4 клеточки, а стало (по Пифагору) 
, т.е. увеличилось в 5,66/4=1,41 раз, во столько же раз уменьшится потенциальная энергия и станет равной 2/1,41=1,42 Дж, абсолютное уменьшение 2-1,42=0,58≈0,6 Дж.
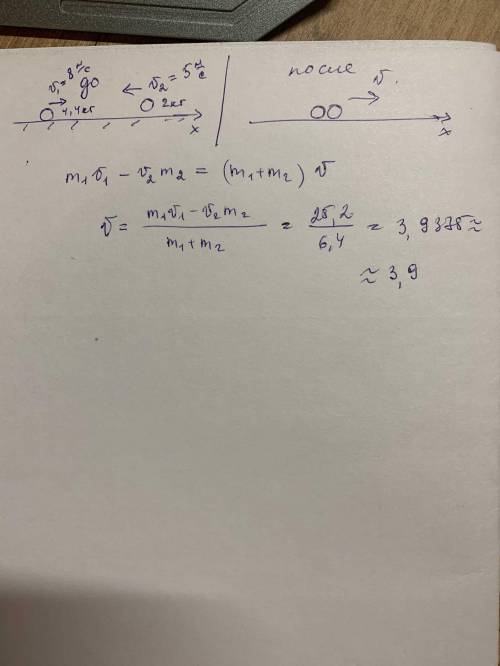
Объяснение:Два пластилиновых шарика массами m1= 4,4 кг и m2= 2 кг движутся по гладкой горизонтальной поверхности вдоль одной прямой навстречу друг другу со скоростями v1= 8 м/с и v2= 5 м/с соответственно. Через некоторое время шарики сталкиваются, склеиваются и далее начинают двигаться как одно тело. Определи скорость шариков после склеивания. (ответы округли до десятых.) Шаг 1. Найди импульс первого шарика до взаимодействия: p1= 4,4*8 кг·м/с=35,2кг·м/с. Шаг 2. Найди импульс второго шарика до взаимодействия: p2= 2*5 кг·м/с=10кг·м/с. Шаг 3. Найди суммарный импульс двух шариков до взаимодействия, учитывая, что шарики движутся навстречу друг другу: p= 35,2кг·м/с-10кг·м/с=25,2 кг·м/с.
Шаг 4. Найди массу тела, которое получается из слипшихся шариков: m= 6,4кг. Шаг 5. Обозначив скорость тела после слипания шариков как v, запиши импульс P тела после взаимодействия: (m1+m2)V=p1⋅p2 Шаг 6. Поскольку два шарика являются замкнутой системой, то для них выполняется закон сохранения импульса: импульс системы до взаимодействия равен импульсу системы после взаимодействия. Составь уравнение согласно закону сохранения импульса: (m1+m2)V=p1⋅p2 — и реши его относительно v с точностью до десятых: v = 3,9м/с.
зная диаметр шара, можно сразу вычислить радиус, и затем найти все остальные параметры сферы, такие как длина окружности, площадь поверхности и объем. радиус шара через диаметр равен его половине. r=d/2
длина окружности сферы через диаметр выглядит как его произведение на число π, поэтому можно вычислить ее напрямую, без производных формул. p=πd
чтобы найти площадь поверхности сферы через диаметр, нужно преобразовать ее формулу, подставив вместо радиуса одну вторую диаметра, тогда площадь поверхности будет равна произведению числа π на квадрат диаметра. s=4πr^2=(4πd^2)/4=πd^2
для того чтобы вычислить объем шара, необходимо возвести радиус в третью степень, умножив его на четыре трети числа π, поэтому вставив в формулу вместо радиуса половину диаметра, получим, что объем шара через диаметр равен v=4/3 πr^3=4/3 π(d/2)^3=(πd^3)/6