57,5 см
Объяснение:
Закон Архимеда:
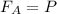, где сила Архимеда 
, ρ₁ - плотность воды, V₁ - объем погруженной части
тела, P - вес тела.
Для одной льдины закон Архимеда:
(1) 
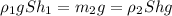, здесь ρ₁ - плотность воды, m₂ - масса льда, ρ₂ - плотность льда, S - площадь горизонального сечения льдины, h₁ - глубина погружения льдины в воду, h - высота льдины.
Отсюда: (2) 
см
Для льдины с медным кубиком:
(3) 
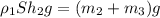, m₂ - масса льда, m₃ - масса медного кубика, h₂ - глубина погружения льдины в воду с установленным медным кубиком.
Подставляем сюда вместо m₂ выражение 1, получаем:
(4) 
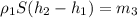, где h₂-h₁ =Δh
Теперь запишем закон Архимеда для льдины с железным кубиком:
, m₂ - масса льда, m₄ - масса железного кубика, H - глубина погружения льдины в воду с установленным железным кубиком.
Подставляем сюда выражение 1:
(5) 
.
Выразим массу железного кубика через массу медного:
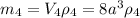, a - длина ребра куба, ρ₄ - плотность железа.
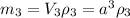, тогда:
(6) 
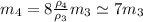
Подставляя (6), (4) в (5):
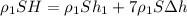
Упрощая это выражение и подставляя из (2) значение h₁:
см.
Очевидно, что значения силы трения покоя в первом и втором случае равны значениям на динамометре. Ведь брусок никуда не двигался, а значит на него действовали равные по модулю силы:
|Fтр покоя1| = |Fт1| => 0,4 Н = 0,4 Н
|Fтр покоя2| = |Fт2| => 0,8 Н = 0,8 Н
А вот когда брусок сдвинулся, сила трения покоя стала максимальной. И в этом случае приложили силу, большую, чем максимальная сила трения покоя (по модулю):
|Fтр покоя max| < |Fт3| => |Fтр покоя3| < 1,2 Н
Далее, если брусок продолжить тащить, то силу тяги можно прикладывать равной по значению максимальной силе трения покоя - движение будет продолжаться равномерно. Эта же максимальная сила трения покоя будет являться уже силой трения скольжения:
|Fтр покоя max| = |Fт3| => 1,2 Н = 1,2 Н
|Fтр скольжения| = |Fт3| => 1,2 Н = 1,2 Н
15<20 значит скорость первого объекта меньше чем скорость второго