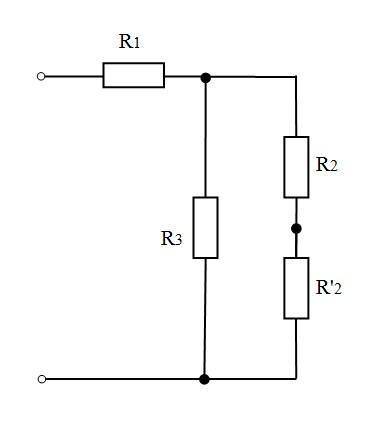
Схема состоит из:
группы сопротивлений R₂ и R₂', соединенных последовательно,
сопротивления R₃, соединенного параллельно с первой группой,
сопротивления R₁, соединенного последовательно с первыми двумя группами.
Преобразовать схему можно так: (см. рис.1)
Тогда общее сопротивление R₂ и R₂':
R₂₂ = R₂ + R₂' = 20 + 20 = 40 (Ом)
То есть сопротивления R₂ и R₂' можно заменить одним сопротивлением R₂₂ = 40 (Ом) (см. рис.2)
Общее сопротивление R₂₂ и R₃:
R₂₂₃ = R₂₂•R₃ : (R₂₂+R₃) = 40•60 : 100 = 24 (Ом)
Общее сопротивление цепи с учетом R₁:
R = R₁ + R₂₂₃ = 6 + 24 = 30 (Ом)
Общий ток в цепи:
I = I₁ = U/R = 240 : 30 = 8 (A)
Напряжение на первом сопротивлении:
U₁ = I · R₁ = 8 · 6 = 48 (B)
Напряжение на группе сопротивлений R₂₂₃:
U₂₂₃ = U - U₁ = 240 - 48 = 192 (B)
Ток, протекающий через R₃:
I₃ = U₂₂₃ : R₃ = 192 : 60 = 3,2 (A)
Ток, протекающий через R₂₂:
I₂₂ = U₂₂₃ : R₂₂ = 192 : 40 = 4,8 (A)
Напряжение на R₂ и R₂':
U₂ = U₂' = R₂I₂₂ = R₂'I₂₂ = 20 · 4,8 = 96 (B)
83.7 (А/м)
Объяснение:
Дано:
I1=90А
I2=70А
r1=12 см
r2=14 см
А=10 см
B=B1+B2
Модуль вектора В по теореме косинусов:
B=√(B12+B22 - 2B1B2cosα)
Магнитные индукции:
B1=μ0I/(2п*r1)
B2=μ0I/(2п*r2)
Подставим выражения в формулу:
B=μ0/(2п)*√(I1^2/r1^2+I2^2/r2^2 - 2*I1*I2*cosα/(r1*r2))
Так как B=μ0H:
H=1/(2п)*√(I1^2/r1^2+I2^2/r2^2 - 2*I1*I2*cosα/(r1*r2))
Теорема косинусов :
A2=r1^2+r2^2 - 2*r1*r2*cosα
cosα=(r1^2+r2^2 - A^2)/(2*r1*r2)
cosα=(12^2+14^2-10^2)/(2*10*15)=240/336=5/7
Вычислим искомую величину:
H=1/(2*3.14)*√(90^2/0.12^2+70^2/0.14^2 - 2*90*70*(5/7)/(0.12*0.14)=83.7 (А/м)
********************************