Eк = (mv^2)/2
A = Nt
A = Fs = Fvt
Nt = Fvt
N = Fv
v = N/F
Eк = (m*N^2)/(2*F^2)
N = √((Eк*2*F^2)/m)
N = √((20*2*25)/2000)
N = 0,7 Вт
28600 В/м
Объяснение:
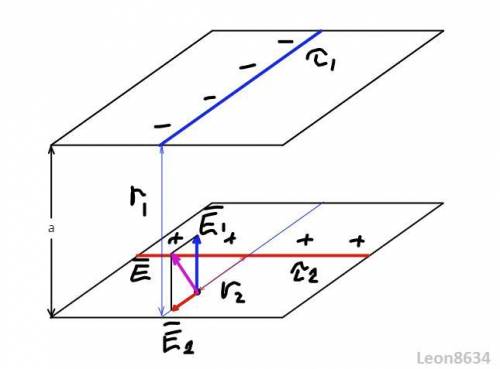
Напряженность поля, создаваемого бесконечной заряженной нитью (выводится на основании теоремы Гаусса):
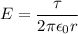
Рассчитаем напряженности от первой и второй нитей:
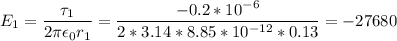 В/м, направлена к нити
В/м, направлена к нити
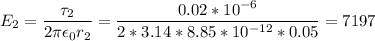 В/м направлена от нити
В/м направлена от нити
Результирующую напряженность поля найдем по теореме Пифагора:
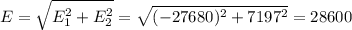 В/м.
В/м.
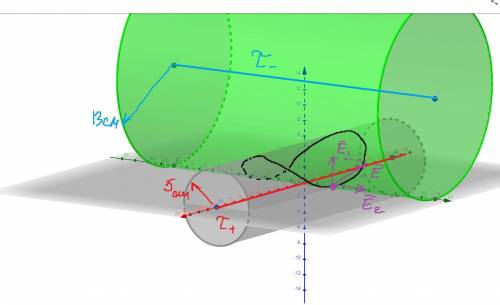
Примечание: На самом деле у этой задачи бесконечно много решений, все точки, удовлетворяющие условию задачи, лежат на кривой пересечения двух цилиндров (см. рисунок). Мы выбрали самую очевидную и простую для расчета точку, она помечена фиолетовым.
Амперметр подключают в цепь, электрический ток проходит через рамку, и на эту рамку со стороны магнитного поля действует сила Ампера. Рамка со стрелкой поворачивается вокруг стального сердечника,из-за этого процесса спиралеобразные пружины закручиваются и создают дополнительную силу упругости. Когда наступает равенство вращательного момента,то поворот рамки прекращается, стрелка останавливается на определенном делении шкалы. Если сила тока увеличится,то и сила Ампера увеличится,которая действует на рамку.
Также работает и вольтметр, просто там электрическое сопротивление намного больше чем у амперметра
тогда Р = F(S\t) или Р= Fv
Р = Fv
Eк = mv^2 \ 2
v = √(2Eк \ m )
v = √(2 * 20 \ 2000) = 0,14 m\c
P = 5 * 0,14 = 0,7 Вт