Условие задачи:
Два тела масс m1 и m2, связанные невесомой нитью, лежат на гладкой горизонтальной поверхности. Нить обрывается, если сила её натяжения превышает значение Tm. C какой максимальной горизонтальной силой F можно тянуть второе тело, чтобы нить не оборвалась?
Задача №2.1.82 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
m1, m2, Tm, Fm−?
Решение задачи:
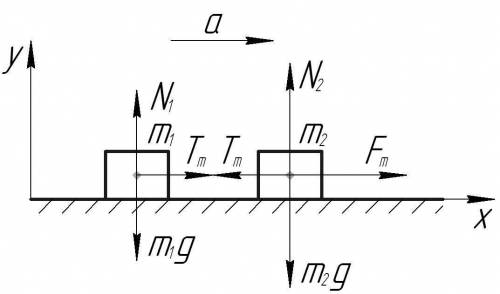
Схема к решению задачиПотянем второе тело с такой силой Fm, что сила натяжения нити, соединяющей тела, станет очень близка по величине к Tm, но ещё не разорвется.
По условию поверхность, по которой движутся тела, гладкая, значит сил трения нет. Покажем на схеме все силы, действующие на тела, потом запишем второй закон Ньютона для обоих тел в проекции на ось x. Ускорения рассматриваемых тел, естественно, одинаковые.
{Fm—Tm=m2aTm=m1a
Сложим оба выражения системы, а из полученного выразим ускорение a.
Fm=(m1+m2)a
a=Fmm1+m2
Подставим формулу в последнее выражение системы, а оттуда выразим искомую силу Fm.
Tm=Fmm1m1+m2
Fm=Tm(m1+m2)m1
Поделим почленно числитель дроби на знаменатель.
Fm=Tm(1+m2m1)
В условии не было дано числовых данных, задачу требовалось решить в общем виде, что мы и сделали.
ответ: Tm(1+m2m1)
v0 = 3 м/с
а = 2 м/с²
Объяснение:
Мы знаем что
s = v0t + ( at² )/2
или
s = v0t + at²0,5
Зная это составим систему
s(1) = v0t(1) + at(1)²0,5
s(2) = v0t(2) + at(2)²0,5
Где а ; v0 постоянные постоянные величины ( ускорение и начальная скорость тела ( соответственно ) ) ( подставим численные значения и решим систему )
40 = v0 5 + a 5² * 0,5
130 = v0 10 + a 10² * 0,5
Упростим
40 = 5v0 + 12,5а
130 = 10v0 + 50a
Разделим обе части уравнения на 5
8 = v0 + 2,5a | * ( -2 )
26 = 2v0 + 10a
-16 = -2v0 - 5a
26 = 2v0 + 10a
Суммируем две системы уравнения ( и получим одно уравнение )
10 = 5a
отсюда
а = 2 м/с²
Подставим численное значение ускорения в уравнение 8 = v0 + 2,5a и решим относительно начальной скорости тела
8 = v0 + 5
отсюда
v0 = 3 м/с