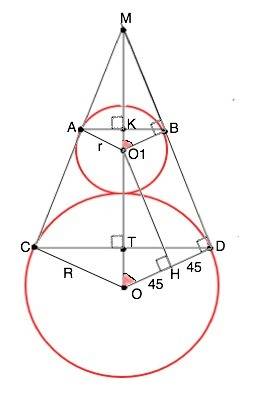
Продлим касательные до их пересечения в точке М.
Центры О и О₁ касающихся окружностей лежат на биссектрисе МО угла СМD.
r =O₁B=45, R=OD=90.
Радиусы О₁В и ОD, проведенные в точки касания, перпендикулярны касательной МD (свойство радиусов).
Из О₁ проведем О₁Н ║ МD. В параллелограмме О₁ВDО ∠В=∠D= 90°, следовательно, О₁ОDВ - прямоугольник.
HD=O₁B, ОН=90-45=45.
Прямоугольные ∆ МО₁В и ∆ МОD подобны по общему острому углу при М.
ОО₁=R+r=90+45=135
Косинус равных углов при О и О₁=ОН/ОО₁=45/135=1/3.
Тогда КО₁=О₁В•cos KO₁B=45•1/3=15
TO=DO•cos TOD=90•1/3=30
Расстояние между АВ и СD равно
КТ=ОО₁-ТО+КО₁=135-30+15=120 (ед. длины)
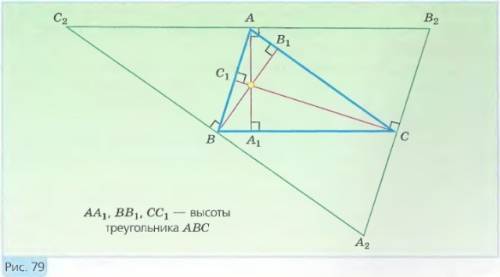
Доказательство. Рассмотрим треугольник ABC с высотами AA1, BB1 и CC1 и докажем, что прямые AA1, BB1 и CC1 пересекаются в одной точке.
Проведем через точки A, B, C прямые, соответственно перпендикулярные к прямым AA1, BB1, CC1 и, следовательно, соответственно параллельные прямым BC, CA, AB (рис. 79). Эти прямые, пересекаясь, образуют треугольник A2B2C2.
Так как C2A || BC и C2B || AC, то четырехугольник BC2AC — параллелограмм, поэтому C2A = BC. По аналогичной причине AB2 = BC. Из этих двух равенств следует, что C2A = AB2, т. е. точка A — середина отрезка C2B2. Аналогично можно доказать, что точки B и C — середины отрезков A2C2 и A2B2.
Таким образом, прямые AA1, BB1, CC1 являются серединными перпендикулярами к сторонам треугольника A2B2C2, поэтому они пересекаются в одной точке. Теорема доказана.
Точку пересечения высот треугольника (или их продолжений) для краткости называют ортоцентром треугольника.
Итак, с каждым треугольником связаны четыре точки: точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам, точка пересечения медиан и ортоцентр. Эти четыре точки называются замечательными точками треугольника.
Объяснение: Сумма всех углов в паралелограмме равна 360°. Противоположные углы равны.(360-110-110)/2=70°
(360-220)/2=140/2=70°
Углы: 110; 70; 110; 70.