Проекции катетов на гипотенузу прямоугольного треугольника - это отрезки гипотенузы, на которые ее делит высота, т.к. высота - перпендикуляр к прямой ( гипотенузе), а катеты – наклонные из вершины прямого угла.
Катет - среднее пропорциональное между гипотенузой и его проекцией на неё .
В треугольнике на рисунке приложения
Катет Вс=30 см, а ВН=18 - его проекция на гипотенузу.
BC²=АВ•НВ
900=АВ•18
АВ=900:18=50 см
Высота, проведенная к гипотенузе, делит прямоугольный треугольник на подобные. Из подобия следует отношение:
АН:АС=АС:АВ
АН=50-18=32
32:АС=АС:50 ⇒ АС²=32•50
АС=√1600=40 см
-----------
Если обратить внимание на отношение катета и гипотенузы 3:5 в ∆ ВСН, увидим, что этот треугольник - египетский. Отсюда следует АВ=50 см, (т.к. меньший катет=30). а АС=40 см. Получим длины сторон треугольника, отношение которых 3:4:5.

См. рис. во вложении
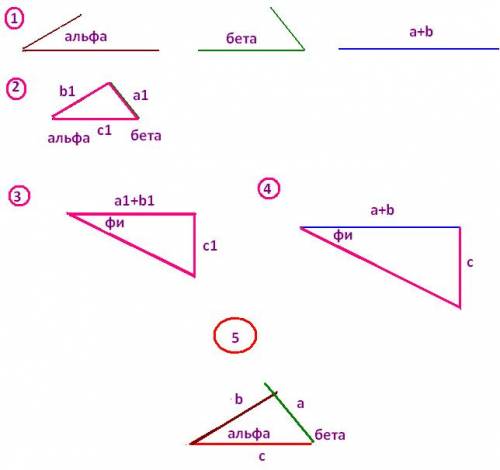
Для построения будем использовать свойста подобия треугольников.
1. Дано: два угла и отрезок.
2. Строим вс треугольник с углами альфа и бета и произвольными сторонами а1 , в1 и с1
3. К отрезку а1+в1 к крайней точке восстанавливаем перпендикуляр длиной с1. Проводим к его концу прямую и получаем угол фи.
4. К отрезку а+в проводим в левой крайней точке луч под углом фи, а справа перпендикуляр. Пересекаясь с перпендикуляром прямая отсечет на ней отрезок с, т.к. треугольники будут также подобны.
5 По двум углам и полученной строне с строим искомый треугольник. Проверяем совпала ли сумма а+в полученных с заданными. Должна совпасть, если все сделали правильно.
на фото
Объяснение: