а) В прямоугольной системе координат уравнение сферы радиуса R с центром в точке С(Xo; Yo; Zo) имеет вид:
(x - xo)² + (y - yo)² + (z - zo)² = R².
Значит, надо выделить полные квадраты в заданном уравнении
x² + y² + z² - 4x + 6y = 36.
(x² - 4x + 4) - 4 + (y² + 6y + 9) - 9 + z² = 36.
(x - 2)² +( y + 3)² + z² = 49.
Теперь видны координаты центра сферы: О(2; -3; 0) и величина радиуса R = √49 = 7.
б) Расстояние от центра сферы до заданной плоскости x = −6 равно 2 - (-6) = 8.
Так как радиус равен 7, то сфера не касается такой плоскости.
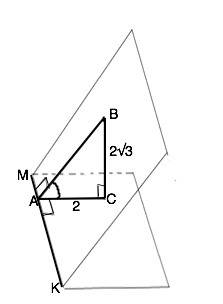
ВС перпендикулярен плоскости, следовательно, перпендикулярен любой прямой, лежащей в этой плоскости и проходящей через его основание С. ⇒ ∆ ВСА - прямоугольный с прямым углом С.
По т.о 3-х перпендикулярах: если наклонная перпендикулярна прямой, лежащей в плоскости, значит, этой прямой перпендикулярна и ее проекция.
ВА - перпендикулярен ребру МК двугранного угла, следовательно его проекция СА перпендикулярна прямой МК.
Величиной двугранного угла является градусная мера его линейного угла.
Линейный угол двугранного угла – угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
АВ и АС перпендикулярны МК. Следовательно, угол ВАC -искомый.
ctg BAC =2:2√3=1/√3 - это котангенс 60°.
Угол ВАС=60°
ответ:
удачи хех)