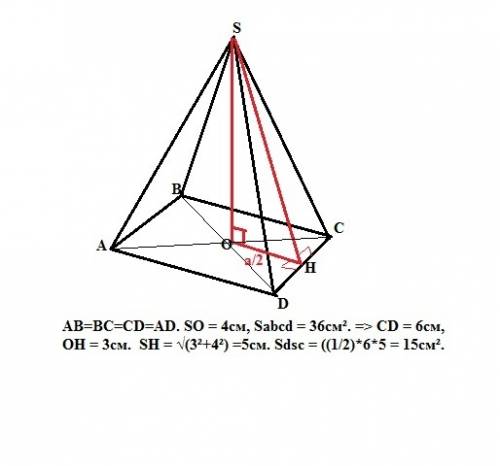
Объем пирамиды: V=(1/3)*So*H, где So - площадь основания пирамиды, H - высота пирамиды. Объем и высота нам даны, найдем площадь основания. So = 48*3/4 = 36 ед². Пирамида правильная, значит в основании лежит квадрат со стороной а = √36 = 6ед, а вершина пирамиды проецируется в центр основания - точку пересечения его диагоналей. Боковые грани нашей пирамиды - равные равнобедренные треугольники. Найдем высоту грани (апофему) из прямоугольного треугольника, образованного высотой пирамиды, половиной стороны основания (катеты) и апофемой (гипотенуза). Ап = √(3²+4²) =5ед.
Тогда площадь одной боковой грани равна Sгр=(1/2)*а*Ап или Sгр=(1/2)*6*5 = 15ед², а площадь боковой поверхности равна
Sбок = 4*Sгр. = 60 ед².
ответ: Sбок = 60 ед².
AB=CD
угол А=уголD (как углы при основании трапеции)
BC=3 cм
AD=9 cм
ВН= 4 см
ВН _I_ AD
Найти Р abcd=?
Решение
Проведем из точки С высоту Н1 к основанию АD
Рассмотрим треугольники АВН и СН1D (прямоугольные)они равны по гипотенузе АВ и СD острым углам А и D (первый признак равества прямоугольных треугольников) . Следовательно равны и их стороны АН и DН1.
АD= АН+НН1+DН НН1=ВС= 3см АН=(9-3)/2=3.
Из треугольника АВН по теореме Пифагора находим чему равна гипот енуза АВ. АВ2=ВН2+АН2 АВ= корень 16+9=5 см
Рadcd= АВ+ВС+СD+AD Р= 5+5+3+9=22 см
ответ Рabcd= 22cм