АВ=9 см
Объяснение:
Пусть отрезок АВ=х см, тогда АС=х-3 и в сумме они дают ВС=15 см. Получим:
х+(х-3)=15
2х-3=18
2х=18
АВ= х=9 см
1. 1. Рассмотрим ΔМСТ.
Так как В-середина МТ, ВС является медианой ΔМСТ.
2. Медиана треугольника разбивает его на два равновеликих треугольника, т.е., с одинаковой площадью.
SΔBCT = SΔMBC
3. Так как МС равна 2/3 АС, SΔМВС = 2/3 SΔАВС.
Значит, SΔBCN = 2/3 SΔABC = 2/3S.
ответ. 2/3 S.
2. 1. Обозначим боковые стороны а и b, основание - с, высоту, опущенную на основание, - h₁. А высоту, опущенную на боковую сторону, которую нужно найти, обозначим h₂.
Находим боковую сторону по теореме Пифагора.
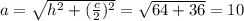 (см).
(см).
2. S=½ ah
ch₁ = ah₂
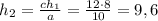 (см)
(см)
ответ. 9,6 см.
3. Наименьшая сторона будет лежать напротив наименьшего угла.
Используем теорему синусов.
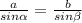
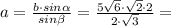 5·2 = 10 (cм)
5·2 = 10 (cм)
ответ. 10 см.
Начерти окружность, обозначь точку В, лежащую вне окружности, проведи через данную точку две касательные, точки касания обозначь А и С , точка О - центр окружности.
Так как касательная перпендикулярна радиусу в точке касания, то мы получили два прямоугольных треугольника ОАВ и СОВ, равных между собой, с меньшими углами 60/2=30 град. и катетами, лежащими против этих углов равными радиусу окружности АО=ОС=12 см,
катет, лежащий против угла 30 град= 1/2 гипотенузы,
следует ОВ=2*АО=24 см, расстояние до окружности=
ОВ-r=24-12=12 cм.
5см
Объяснение:
15:3=5см.- відрізок АВ