В условии опечатка: надо доказать, что ΔBDC равнобедренный.
ΔBDC равнобедренный,
AD < DC.
Пошаговое объяснение:
а) Зная, что сумма углов треугольника 180°, найдем угол АВС:
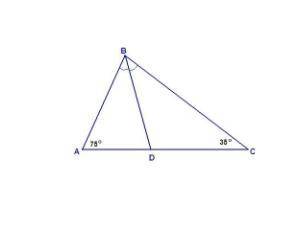
∠АВС = 180° - (∠А + ∠С) = 180° - 110° = 70°
Так как BD биссектриса угла АВС, то
∠ABD = ∠CBD = 70°/2 = 35°.
В треугольнике BDC два угла равны, значит он равнобедренный по признаку равнобедренного треугольника.
б) В треугольнике напротив меньшего угла лежит меньшая сторона.
В ΔABD AD < BD, так как AD лежит напротив угла 35°, а BD напротив угла в 75°.
Но BD = DC (доказано выше), тогда
AD < DC
надеюсь , если да то можешь пометить лучшим ответом
ответ: 6,5 см: 11,5 см
Объяснение:
Пусть точка С лежит на АВ.
Примем АС=х, тогда ВС=х+5.
По условию АС+ВС=АВ
х+х+5=18,
2х=18-5,
2х=13; х=13/2=6,5 см,
Ас=6,5 см ВС=6,5+5=11,5 см