Дано:
Усеченный конус
Sосн₁ = 9π см²
Sосн₂ = 100π см²
Sсеч = 312π см²
--------------------------------
Найти:
h - ?
1) Сначала мы найдем радиусы окружности верхнего и нижнего усеченного конуса используя площадь круга:
Sосн₁ = πr² ⇒ r = √Sосн₁/π = √9π см²/π = √9 см² = 3 см ⇒ BO₁ = BC = 3 cм
Sосн₂ = πR² ⇒ R = √Sосн₁/π = √100π см²/π = √100 см² = 10 см ⇒ AO = OD = 10 см
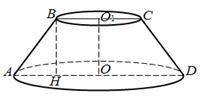
2) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса: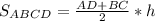 
3) В трапеции ABCD:
AD = 2AO = 2R = 2×10 см = 20 см
BC = 2BO₁ = 2r = 2×3 см = 6 см
4) И теперь находим высоту равнобедренной трапеций ABCD:
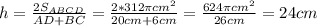⇒ h = OO₁ = BH = 24 см
ответ: h = 24 см
P.S. Рисунок показан внизу↓
LC=6, AK=3√2 (три квадратных корня из двух)
Объяснение:
1. угол С равен углу А по свойству параллелограмма
2. Рассмотрим треугольник ВCL
Угол СBL будет равен угол BLC минус угол
90-45=45°
Следовательно треугольник BCL прямоугольный и равнобедренный.
Т.к. треугольник равнобедренный, то CL=BL=6
3. По теореме Пифагора BC²=BL²+CL²
BC²=72
BC=√72=√36*2=6√2
4. Т.к. BK медиана, 2АК=6√2
АК=3√2