Вариант 5 п. постройте квадрат и проведите его диагонали. запишите свойства квадрата. 2. в ромбе abcd - id1007075120230227 от polinaponomare1 27.02.2023 05:04

Question

Геометрия: Вариант 5 п. постройте квадрат и проведите его диагонали. запишите свойства квадрата. 2. в ромбе abcd 0 - точка пересечения диагоналей ac и bd. угол abc равен 100°. найдите углы треугольника cod 3. дан отрезок kl. с чертежных инструментов постройте точку р так, чтобы кр : ple 2.1. 4. в треугольнике abc со сторонами 10см и 12см и 14см средняя линия mn отсекает от него трапецию amnc. найдите периметр треугольника mbn сор

polinaponomare1 · Accepted Answer

Если точка С - середина отрезка АВ, то ее координаты (х ; у) находятся по формуле:
x = (x₁ + x₂)/2 y = (y₁ + y₂)/2.

1) A ( - 3 ; 4), B ( 2 ; - 2)
x = (- 3 + 2)/2 = - 1/2 = - 0,5
y = (4 - 2)/2 = 1
C(- 0,5 ; 1)

2) A ( - 1 ; - 7), B ( - 4 ; 3)
x = (- 1 - 4)/2 = - 5/2 = - 2,5
y = (- 7 + 3)/2 = - 4/2 = - 2
C (- 2,5 ; - 2 )

3) A ( 2,8 ; - 6), B ( - 3 ; 1,6)
x = (2,8 - 3)/2 = - 0,2/2 = - 0,1
y = (- 6 + 1,6)/2 = - 4,4/2 = - 2,2
C(- 0,1 ; - 2,2)

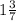4) A ( $1 \frac{3}{7}$ ; 0), B ( 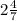$2 \frac{4}{7}$ ; 5).
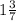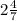x = ( $1 \frac{3}{7}$ + $2 \frac{4}{7}$ )/2 = 4/2 = 2
y = (0 + 5)/2 = 2,5
C(2 ; 2,5)

MOGZ ответил