Дано: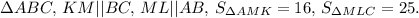 
Найти: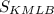 
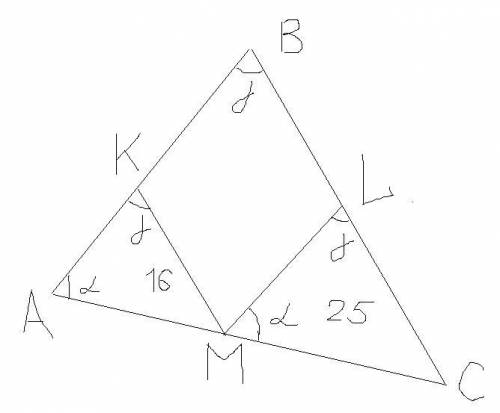
Решение: Заметим, что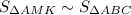 
по двум углам. Один угол общий, 
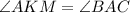- как односторонние углы при параллельных прямых КМ и ВС и секущей ВК.
Также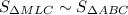 
по двум углам. Один угол общий, 
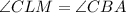- как односторонние углы при параллельных прямых LМ и AВ и секущей ВC.
Значит, по свойствам подобия треугольников
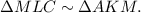
Вычислим коэффициент подобия этих треугольников
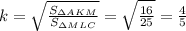
Заметим также, что
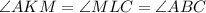- по свойству параллельных прямых.
По свойству параллелограмма ML=KB. По свойству подобия треугольников
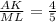
Пусть АК=4х, тогда КВ=ML=5x. AK+KB=AB=4x+5x=9x.
Значит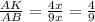 
- это коэффициент подобия треугольников AKM и AВС. Вычислим площадь теугольника АВС.
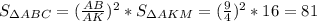
По своствам площадей
Подставим известные значения
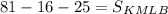
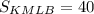
ответ: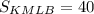
ответ:
объяснение:
1. рассмотрим параллелограмм авсд.
s=ah, а= 6 это следует h=4
2.рассмотрим δ аве, в=5, h=4. тогда по теореме пифагора
хво2степени =5 в степени2 - 4 в степени2 =9
х=3, т.е. ае=дк=3, это следует
3. ед=ад-ае=3
4. рассмотрим δвед, по теореме пифагора следует
хво 2 степени=3во 2степени+4во второй степени=25
×=5,т.е. вд=5
5.проведем дополнительную высоту ск с вершины с и соединяем с основанием ад
6. рассмотрим δ аск, ак=9, ск=4⇒ по теореме пифагора
хво 2степени=9во2степени+4 во 2степени=97
×=√97, т.е. ас=√97