Объяснение:
Тангенс угла в прямоугольном треугольнике - это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
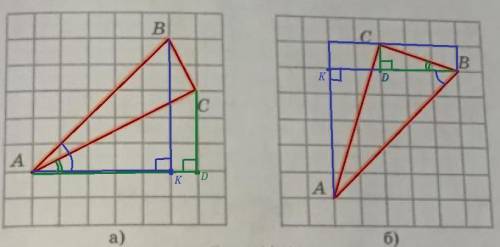
а)
tg∠A = BC / AC = 3/6 = 1/2
ctg∠A = AC / BC = 6/3 = 2
б)
tg∠B = AC / BC = 4/6 = 2/3
ctg∠B = BC / AC = 6/4 = 3/2
№2
Тангенс угла в прямоугольном треугольнике -это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
tg(a-β)=tga-tgβ/1+tga×tgβ; tg(a+β)= tga+tgβ/1-tga×tgβ
a)tg ∠BAC = tg(∠BAD-∠CAD) =tg∠BAD- tg-∠CAD/1+tg∠BAD×tg∠CAD=∠BAD= BK/AK=5/5=1; tg∠CAD= CD/AD=3/6=1/2=1-1/2/1+1×1/2=1/2/3/2=1/3
ctg∠BAD=1/tg∠BAD=1/1/3
b) tg∠ABC=tg(∠CBD+∠KBA) =tg∠CBD+tg∠KBA/1-tg∠CBD×tg∠KBA=tg∠CBD=CD/BD=1/3; tg∠KBA=AK/BK=5/5=1=1/3+1/1-1×1/3=4/3/2/3=4/2=2
О- точка пересечения серединных перпендикуляров ( ОМ, ОN и АО)
следовательно, точка пересечения серединных перпендикуляров делит треугольник на шесть равных треугольников
следовательно, треугольник АВС - равносторонний
найдем угол МОА
ОН - является высотой для стороны ВС и делит угол ВОС пополам
следовательно, угол ВОН равен 30 градусов
рассмотрим прямую НА = 180 градусов
следовательно, угол ВОА равен 150 градусов
следовательно, угол МОА равен 150-90=60 градусов ( т.к. угол ОМА = 90)
следовательно, найдем угол МАО = 180-(90+60)=30
рассмотрим треугольник МАО
сторона лежащия на против угла в 30 градусов , равна половине гипотенузы , следовательно сторона МО = 12
по теореме Пифагора найдем сторону АО = 21
рассмотрим треугольник АВН
ВН=12
АН=42
АВ^2 = корень из 42^2+12^2
АВ = 40
АВ=ВС=40
ВС=40
Возможно кто-то напишет простое решение ( возможно это не совсем правильно)
в 4 раза
Объяснение:
по теореме Черномора