Объяснение:
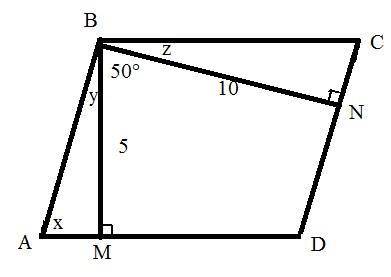
Пусть ABCD - параллелограмм. BM=5см и BN=10см - высоты, проведённые из вершины В. Для простоты пусть <BAM=x, <ABM=y, <CBN=z.
В прямоугольном тр-ке △АВМ х+у=90°.
<ABC=y+50°+z.
По свойству углов параллелограмма <BAD+<ABC=180°. Подставляем наши значения:
х+y+50+z=180
Подставляем сюда выражение для х+у:
90+50+z=180
z=40°
cosCBN=BN/BC; BC=BN/cos40°=10/0,766=13,06 см
y=z, поскольку <BAM=<BCN
cosABM=BM/AB; AB=BM/cos40°=5/0.766=6.53 см
Либо можно воспользоваться свойством, что угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма, и получить те же значения.
Итак, если два угла равны, то треугольник равнобедренный.
Осталось найти третью сторону.
Каждая сторона треугольника меньше суммы двух других сторон.
Допустим, боковая сторона равна 25 см, тогда 25 см+25 см > 40 см ;
40 см+25 см > 25 см ; 40 см+25 см > 25 см.
Теперь пусть боковая сторона равна 40 см. Тогда 40 см+40 см > 25 см ; 40 см+25 см > 25 см ; 40 см+25 см > 25 см.
Тогда, в первом случае периметр равен 25см+25см+40см = 90см, а во втором 40см+40см+25см = 105 см.
ответ: 105 см или 90 см.
ответ:
ответ во вложении.pdf