1. Треугольник называется равнобедренным, если любые две его стороны равны.
2. В равнобедренном треугольнике высота, проведённая к основанию является биссектрисой и медианой.
3. При пересечении двух прямых образовалось четыре угла. Один из углов равен 53 градуса . Найти остальные три угла.
ответ: другой, вертикальный к нему же равен 53°. Смежные с ним углы будут равны 180°-53°=127°. Этих углов тоже два.
4. Основание равнобедренного треугольника 14 см, а периметр 66 см. Найти длины боковых сторон треугольника.
ответ: (66-14):2=26 см длины боковых сторон треугольника.
5. Один из смежных углов на 24 градуса больше другого. Найти эти углы. ответ: Пусть х градусов мера одного угла, тогда (х+24)° - мера второго угла. Тогда сумма смежных углов равна 180°.
х+х+24°=180°
2°+24°=180°
2х°=180°-24°
2х=156°
х=156°:2
х=78° мера одного смежного угла.
78°+24°=102° мера второго смежного угла.
6. Градусные меры смежных углов относятся как 2:7. Найти эти углы. ответ: Пусть 2х - мера одного угла, тогда 7х - мера другого угла. Тогда их сумма равна 180°.
2х+7х= 180°
9х=180°
х=180°:9
х=20°.
Тогда первый угол равен 2х=2*20°=40°, второй угол равен 7х=7*20°=140°.
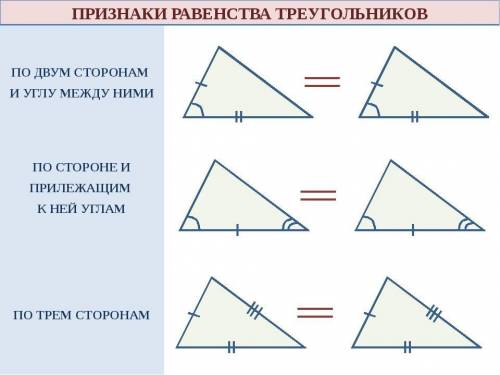
7.Сформулируйте 2 признак равенства треугольников и начертите рисунок к нему
Решение в приложении. Там 3 рисунка.
Тогда 12 х (м) - боковая сторона
Известно, что Р=10 м.
Уравнение:
х+12 х+12 х=10 м
25 х=1000 см
х=1000:25
х=40 см
ответ: основание треугольника = 40 см = 0,4 м.
2. Пусть х (см) - одна сторона
Тогда (х+6) (см) - вторая сторона
Известно, что периметр = 60 см
(х+6) + (х+6) + х + х = 60
4 х = 60 - 12
4 х = 48
х = 48 : 4
х = 12 (см) - одна сторона.
12 см + 6 см = 18 см - вторая сторона.
S = 18 см * 12 см =
ответ: S =
3. 34 - (15 + 15) = 4 (см) - две другие стороны.
4 : 2 = 2 (см) -другая сторона.
ответ: другая сторона прямоугольника = 2 см.
4. Пусть х (см) - одна сторона.
Тогда (5+х) (см) - другая сторона.
Известно, что P = 42 см.
Уравнение:
х + х + (5+х) + (5+х) = 42
4 х = 42 -10
х = 32 : 4
х = 8 (см) - одна сторона.
8 см + 5 см = 13 см - другая сторона.
S = 8 * 13 =
ответ: S =