1. Сумма углов в любом треугольнике равна 180°. Найдем угол A: 180 - ( 56 + 64 ) = 60°.
BC = 3√3 ( по условию ), противолежащий угол A = 60°.
По теореме синусов:
(3√3) / sin 60° = 2R
(3√3) / (√3/2) = 2R
6 = 2R
R = 3.
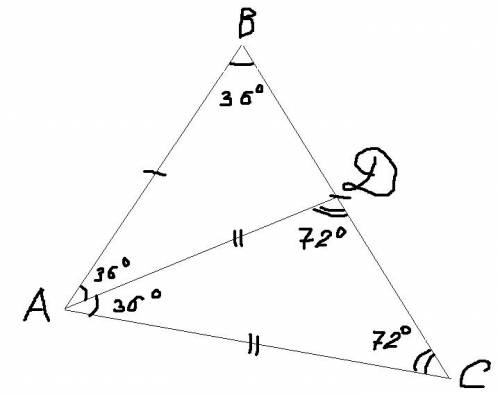
2. В равнобедренном треугольнике углы при основании равны. Найдем углы при основании треугольника ABC: (180 - 36) / 2 = 72°.
Значит угол BAC = BCA = 72°.
AD - биссектриса, делит угол BAC на два равных угла: BAD = DAC = 36°.
В треугольнике ADC нам известны два угла: DAC = 36°, DCA = 72°. Найдем третий угол:
180 - ( 72 + 36 ) = 72. Значит треугольник ADC - равнобедренный, так как углы при его основании равны.
1) Первая задача решается немного легче на мой взгляд. Стоит вспомнить теорему синусов в расширенном виде.
Здесь
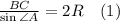
R - искомый радиус окружности.
Теперь надо найти угол А. Сумма углов в треугольнике равна 180 градусам.
Остальные два угла известны по условию задачи.
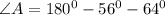
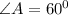
Подставим в (1)
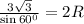
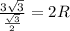
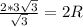
сократим на 2 обе части

R=3.
2) Докажем, что треугольник ACD - равнобедренный. Смотри рисунок во вложении. Так как АВ=ВС, то углы ВАС и ВСА равны. Вычислим сколько градусов составляют эти углы. Сумма всех углов в треугольнике равна 180 градусам. В самом треугольнике АВС
Пусть
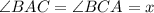
180=x+x+36
180=2x+36
2x=180-36
2x=144
x=72
Так как AD - биссектриса, то
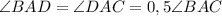
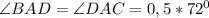
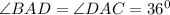
Теперь знаем два угла в треугольнике ADC.
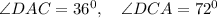
По той же теореме о сумме углов в треугольнике
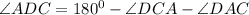
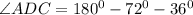
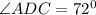
Получается, что
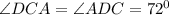
Значит два угла в треугольнике ACD - равны, поэтому треугольник равнобедренный.
Дано : ABCD-параллелограмм
d1=12
d2=17
a=30°
Найти : S-?
Решение.
Площадь параллелограмма через длины его диагоналей d1=12 и d2=17 можно найти по формуле:
S=1/2× d1×d2×sin a
где α=30° - угол между ними. Подставляем числовые значения в формулу, получаем:
S=1/2× 12×17×sin 30°(0.5)=102×0.5
51
ответ: 51.