5 номер
В равнобедренном треугольнике две стороны равны.
По неравенству сторон треугольника знаем, что сумма двух сторон треугольника не может быть меньше третьей.
Предположим, что третья сторона равна 4 см.
Проверим, 4+4<9 - не подходит.
9+9>4 - подходит, значит, третья сторона = 9 см
6 номер
1)Рассмотрим треугольник DME:
предположим ,что угол DME - тупой (будет смежным с острым углом этого треугольника) и
угол DEM - острый (так как двух углов тупых не может быть в треугольнике по определению и признаку треугольника) .
2)Если напротив большего угла в данном треугольнике лежит самая большая сторона,то DE>DM.
7 номер
<B = 180° - (79°+ 55°)= 46° .
<C = 180° - ( 46° + 55°) = 79° .
< А = 55° (по условию).
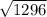 =36
=36
В, 50%
Объяснение:
Возьмём за радиус R. Так как маленькая окружность касается большую, проходит через её центр, то получим, что радиус маленькой окружности в два раза меньше радиуса большой окружности r=R/2
По формуле длины окружности: c=2*π*R получим длины обеих окружностей.
c1=2*π*R
c2=2*π*r=2*π*(R/2)=π*R
Длины окружностей отличаются в два раза, значит маленькая окружность составляет половину большой.