Высота остроугольного треугольника равна 12 см. На каком расстоянии от вершины нужно провести прямую, перпендикулярную этой высоте, чтобы площадь треугольника разделить пополам?
ответ: D) 6√2
——————
Объяснение (подробно).
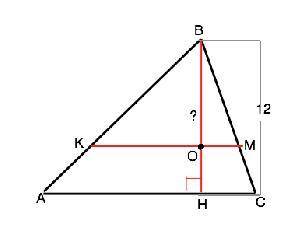
Назовем данный треугольник АВС. Высота ВН треугольника перпендикулярна стороне АС , к которой проведена. Прямая КМ перпендикулярна высоте.
Если две прямые на плоскости перпендикулярны одной и той же прямой, то они параллельны.
МК параллельна стороне АС, к которой проведена высота, и отсекает от треугольника АВС подобный ему ∆ КВМ по равным углам ( угол при вершине общий, соответственные углы при пересечении параллельных прямых АС и КМ секущими АВ и СВ равны).
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Ѕ(КВМ):Ѕ(АВС)=k²=1/2
k=√(1/2)=√(2/4)=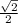 
Отношение линейных размеров сходственных элементов подобных фигур равно коэффициенту их подобия.
Отношение высоты ВО в ∆ КВМ к высоте ВН в ∆ АВС равно k=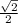
BO:12=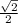 => ВО= (12√2):2=6√2 - искомое расстояние.
1 способ. можно воспользоваться правилом, что синус угла от 0° до 90° возрастает, синус угла от 90° до 180° убывает.
а) sin 150°; sin 135°; sin 90° ; sin 60°
в) использовать формулу , чтобы свести все углы в первую четверть.
sin (180° - α) = sin α
sin 60° = sin (180° - 60°) = sin 120°
sin 90° = sin (180° - 90°) = sin 90°
sin 135° = sin (180° - 135°) = sin 45°
sin 150° = sin (180° - 150°) = sin 30°
ответ: sin 150°; sin 135°; sin 90° ; sin 60°
по таблице косинусов углов
cos(0°)=cos(0)= 1
cos(60°)=cos(π/3)=1/2
cos(90°)=cos(π/2)= 0
cos(135°)=cos3 x π/4=,7071)
cos(150°)=cos5 x π/6=(-0,8660)
ответ cos(150°). cos(135°). cos(90°). cos(60°)