Уравнение прямой имеет вид: y = kx + b
1) Прямая проходит через точки (0;0) и (2;-8). Подставим координаты точек в уравнение прямой. Так как прямая проходит через начало координат, то b = 0.
-8 = k*2; k = -4; уравнение прямой y = -4x.
2) (0;6); (6;-6)
6 = k*0 + b ⇒ b = 6;
-6 = k*6 + 6; -12 = 6k; k = -2.
уравнение прямой y = -2x + 6.
3) (0;-5) (-10: 0)
-5 = k*0 + b ⇒ b = -5;
0 = k*(-10)-5; k = -0,5;
уравнение прямой y = -0,5x -5.
4) (5;-1) (-3;2)
-1 = 5k + b
2 = -3k + b
Решим систему уравнений. Вычтем из 1-го уравнения второе.
-1-2 = 5k+3k; -3 = 8k; k = -3/8;
b = -1 -5 *(-3/8) = -1 +15/8 = 7/8;
уравнение прямой y = (-3/8)x + 7/8.
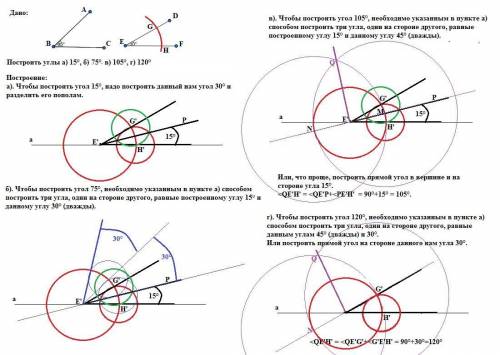
Построение:
а). Чтобы построить угол 15°, надо построить данный нам угол DEF = 30° и разделить его пополам.
Построение угла, равного данному:
1. Из точки Е, как из цкнтра, проводим дугу произвольного радиуса R до пересечения со сторонами угла DE и FE в точках G и H соответственно.
2. На прямой "а" ставим точку Е' и проводим из этой точки дугу радиуса R. В точке пересечения с прямой "а" ставим точку Н'. Из этой точки проводим дугу радиуса GH и в точке пересечения двух дуг ставим точку G'. Через точки E' и G' проводим прямую.
Построен угол G'E'H', равный данному.
Построение угла, равного 15°:
1. Строим биссектрису угла G'E'H'. Для этого:
циркулем проводим окружность с центром в точке G' радиусом G'H'=GH и затем проводим прямую через точку E' и точки пересечения окружностей радиуса GH прямой E'P. Эта прямая - биссектриса угла G'E'H', (точка Р равноудалена от сторон этого угла, так как E'P - серединный перпендикуляр к отрезку G'H' по построению).
Следовательно, <E"E'H' = <E"E'G' =15°.
б). Чтобы построить угол 75°, необходимо указанным в пункте а построить три угла, один на стороне другого, равные построенному углу 15° и данному углу 30° (дважды).
в). Чтобы построить угол 105°, необходимо указанным в пункте а построить угол, равный построенному углу 15° и построить на его стороне угол, равный 90°.
Чтобы построить прямой угол на стороне угла 15°, надо построить перпендикуляр к стороне угла в его вершине. Для этого отметим точку М в месте пересечения стороны PЕ' построенного угла 15° с окружностью и продлим эту сторону до пересечения с окружностью в точке N и из точек M и N.
Или построить три угла указанным в пункте а один на стороне другого, равные построенному углу 15° и данному углу 45° (дважды).
г). Чтобы построить угол 120°, необходимо указанным в пункте а построить три угла, один на стороне другого, равные данным углам 45° (дважды) и 30°.
Или, что проще, построить прямой угол на стороне данного нам угла 30°.
P.S. Все построения подробно расписаны в пунктах, где они встречаются впервые.
BD - диагональ ромба и ∠ABD = ∠ADB. Обозначим ∠OBD = α. Так как OB - биссектриса, то ∠ODB = 2α. Рассмотрим треугольник BOD и запишем сумму его углов: 153° + α + 2α = 180° => 3α = 27° => α= 27°/3 = 9°. Значит ∠ABD = 2α = 18°. Запишем сумму углов в треугольнике DAB: ∠DAB + 4α= 180° => ∠DAB = 180° - 36° = 144°. ∠DCB = ∠DAB = 144°.