Внимание : тут два варианта .
56 или 52 см
Объяснение:
Вариант 1 (если бисс АК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг АВК–равнобед =>АВ=ВК=10 и =СD (как стороны парал);
2) ВС=18+10=28=АD;
3) Р =( 18+10)*2=56 см
Вариант 2 (если бисс DК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг DСК–равнобед =>DС=СК=8 и =АВ (как стороны парал);
2) ВС=18+8=26=АD;
3) Р =( 18+8)*2=52
Чертёж в приложении.
Если что-то непонятно , пишите в комментах.
Успехов в учёбе! justDavid
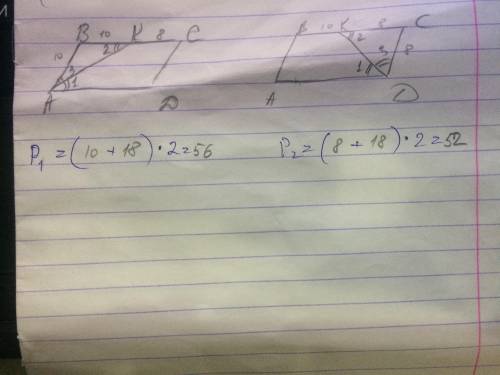
Дано:
тр АВС - р/б (АС - основание)
АМ, СК - медианы
АМ ∩ СК = О
Доказать:
тр АОК = тр СОМ
Доказательство:
1) Т.к тр АВС - р/ б и АМ и СК медианы по условию, то
а) АК=КВ=ВМ=МС
б) уг ВАС = уг ВСА (по св-ву углов при основании р/б тр)
2) тр АКС = тр СМА по двум сторонам и углу между ними, так как в них:
АС - общая сторона
АК = СМ (по п.1а)
уг КАС = уг МСА (по п.1б)
Следовательно, уг АКС = уг СМА и уг АСК = уг САМ
3) уг МАК = уг КСМ, как разность равных углов за минусом равных углов, по аксиоме измерения углов,
а именно уг МАК = уг ВАС - уг САМ и
уг КСМ = уг ВСА - уг АСК
4) Получили:
АК = СМ (из п 1а)
уг МАК = уг КСМ (из п 3)
уг АКС = уг СМА ( из п 2)
следовательно, тр АОК = тр СОМ по стороне и двум прилежащим к ней углам