3в. МА = 3 ед.
4а. АМ = 2 ед.
Объяснение:
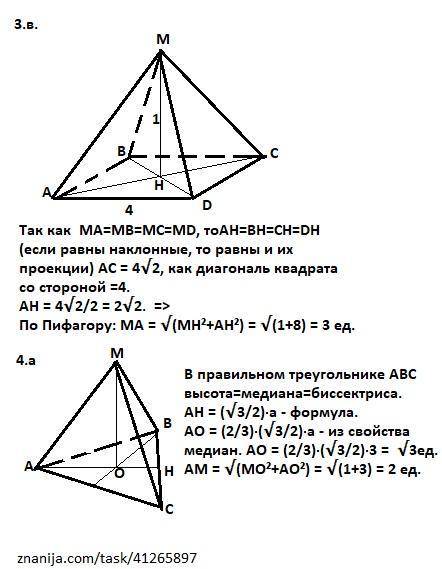
3в. Так как МА=МВ=МС=МD, тоAH=BH=CH=DH (если равны наклонные, то равны и их проекции) АС = 4√2, как диагональ квадрата со стороной =4.
АН = 4√2/2 = 2√2. (половина диагонали) =>
По Пифагору: МА = √(МН²+АН²) = √(1+8) = 3 ед.
4а. В правильном треугольнике АВС высота=медиана=биссектриса.
Центр этого треугольника лежит на пересечении высот (медиан, биссектрис). Медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
АН = (√3/2)·а - формула.
АО = (2/3)·(√3/2)·а - из свойства медиан. АО = (2/3)·(√3/2)·3 = √3ед.
АМ = √(МО²+АО²) = √(1+3) = 2 ед .
Длины всех ребер правильной шестиугольной призмы равны. Вычислителе длину большей диагонали призмы, если известно, что площадь боковой поверхности призмы равна 96 см².
Площадь боковой поверхности правильной шестиугольной призмы находится по формуле:
а - ребро нашей призмы.
Обратим внимание на чертеж. Искомая длина большей диагонали есть длина гипотенузы прямоугольного треугольника АА₁D.
AD = 2 * 4 = 8 (см)
По теореме Пифагора:
с² = a² + b²
AD₁² = AD² + DD₁²
AD₁² = 8² + 4²
AD₁² = 64 + 16
AD₁² = 80
AD₁ = √(16*5) = 4√5 (см)
ответ: 4√5 см