а) Координаты середины отрезка равны полусуммам соответствующих координат его концов.
А (2; -1; 0), В (-4; 2; 2)
Обозначим середину отрезка АВ буковой К
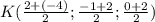
К (-1; 0,5; 1)
б) Нужно найти координаты точки С, если точка В является серединой отрезка АС. Координаты точек А и В известны. Координаты точки С обозначим (x; y; z). И используем формулу для нахождения координат середины отрезка. Находим координаты середины отрезка АС.
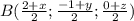
Координаты точки В известны. Приравняем их и получим три уравнения, решая которые найдем координаты точки С.
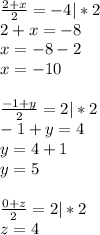
C (-10; 5; 4)
в) Длина отрезка можно вычислить так: квадратный корень из суммы квадратов разностей соответствующих координат концов отрезка.
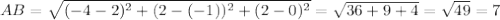
АВ=7
24 м
Объяснение:
В равностороннем треугольнике точка пересечения высот является и точкой пересечения медиан
Если провести медиану к стороне, параллельной проведенной прямой, то точка пересечения медиан поделит эту медиану в отношении 2:1
По теореме о пропорциональных отрезках точки пересечения проведенной прямой с двумя другими сторонами треугольника также делят эти стороны в отношении 2:1
Получаем, что отсеченный треугольник подобен исходному с коэффициентом 2/3, все его стороны в 1.5 раза меньше сторон исходного треугольника, значит, и периметр в 1.5 раза меньше
Поэтому периметр исходного треугольника 16*1.5 = 24 см