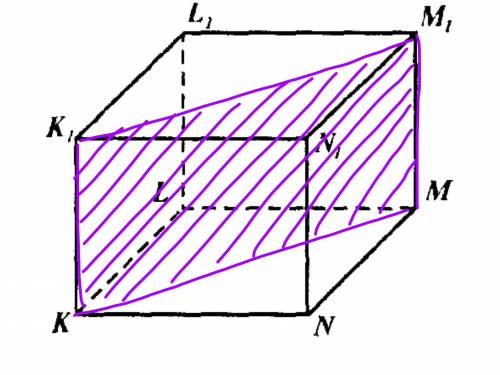
В плоскости К1L1M1N1 линией сечения заданной плоскостью будет отрезок РС, параллельный диагонали L1N1 и равный её половине.
Диагональ параллелепипеда К1М и заданная плоскость пересекутся в диагональной плоскости КК1М1М по линии КД. Точка Д - это середина отрезка РС. Точка Д делит диагональ К1М1 в отношении 1:3.
В сечении получили подобные треугольники К1ЕД и КЕМ.
Коэффициент подобия равен 3/4.
В таком отношении заданная секущая плоскость разделит диагональ К1М.
ответ: плоскость сечения делит диагональ МК1 в отношении 3:4.
Построение:
1) Соединим точки КМ;
2) Грани KLMN и K₁L₁M₁N₁ — параллельны, поэтому построим прямую в плоскости K₁L₁M₁N₁ параллельную прямой КМ через точку М₁;
3) В точке пересечения этой прямой и ребра отметим точку, данная точка уже есть — это точка К₁
Доказательство:
1) Противоположные стороны построенного сечения являются противоположными ребрами параллелепипеда, значит они равны и параллельны;
2) Вторая пара сторон является диагоналями противоположных (граней параллелепипеда, значит они также равны и параллельны;
3) Следовательно построенные сечения являются параллелограммами, что и требовалось доказать.
Объяснение:
1) 4 +6+7+9 = 26 частей
104 \ 26 = 4 см приходится на одну часть
4 * 9 = 36 см - наибольшая сторона
2) 1 + 4+5+8 = 18 частей
360 °\ 18 = 20 ° - приходится на одну часть
20 * 4 = 80°
20 * 5 = 100°
20 * 8 = 160°
3) х - меньшая сторона
3х - большая сторона
( х +3х) * 2 = 64
8х = 64
х = 64 \ 8 = 8 см - наименьшая сторона
4) 4) ( 12 + 22) \ 2 = 17 см - средняя линия трапеции
5) ∠А = ∠С = 360 - 262 = 98°